题目内容
8.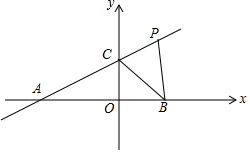 若直线y=$\frac{1}{2}$x+2分别交x轴、y轴于A、C两点,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,且S△ABC=6
若直线y=$\frac{1}{2}$x+2分别交x轴、y轴于A、C两点,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,且S△ABC=6(1)求点B和点P的坐标;
(2)过点B作直线BQ∥AP,交y轴于点Q,求点Q的坐标和四边形BPCQ的面积.
分析 (1)利用一次函数图象上点的坐标特征可求出点A、C的坐标,根据S△ABC=6可求出点B的坐标,再利用一次函数图象上点的坐标特征可求出点P的坐标;
(2)由PB⊥x轴可得出PB∥CQ,结合BQ∥AP可得出四边形BPCQ为平行四边形,再根据点B、C、P的坐标即可得出点Q的坐标以及四边形BPCQ的面积.
解答 解:(1)当x=0时,y=$\frac{1}{2}$x+2=2,
∴点C的坐标为(0,2);
当y=$\frac{1}{2}$x+2=0时,x=-4,
∴点A的坐标为(-4,0).
设点B的坐标为(m,0),
则S△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×[m-(-4)]×2=6,
解得:m=2,
点B的坐标为(2,0).
当x=2时,y=$\frac{1}{2}$x+2=3,
∴点P的坐标为(2,3).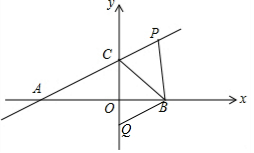
(2)∵PB⊥x轴,
∴PB∥CQ.
∵BQ∥AP,
∴四边形BPCQ为平行四边形.
∵点C(0,2),点B(2,0),点P(2,3),
∴点Q的坐标为(0,-1).
∴S平行四边形BPCQ=OB•BP=2×3=6.
点评 本题考查了一次函数图象上点的坐标特征、三角形的面积、平行四边形的判定与性质以及平行四边形的面积,解题的关键是:(1)根据S△ABC=6求出点B的坐标;(2)根据PB∥CQ、BQ∥AP证出四边形BPCQ为平行四边形.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
7.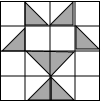 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )
如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,每块方砖大小、质地完全一致,那么它最终停留在黑色区域的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
18.东岳中学初四年级进行了一次模拟考试,参加人数为1016人,为了了解这次考试的成绩情况,下列抽取样本合理的是( )
| A. | 抽取前100名学生的成绩 | B. | 抽取后100名学生的成绩 | ||
| C. | 抽取(1)(2)两个班的学生成绩 | D. | 抽取学号为4的倍数的学生的成绩 |
 如图,正方形ABCD和正方形DEFG的顶点A在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B、C和边EF的中点M,若正方形ABCD的边长为2,则正方形DEFG的面积为$\frac{32}{9}$.
如图,正方形ABCD和正方形DEFG的顶点A在y轴上,顶点D、F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B、C和边EF的中点M,若正方形ABCD的边长为2,则正方形DEFG的面积为$\frac{32}{9}$.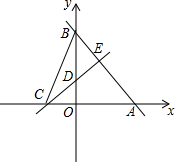 如图,直线y=-$\frac{4}{3}$x+8分别交x轴、y轴于A,B两点.线段AB的垂直平分线分别交x轴、y轴于C,D两点.
如图,直线y=-$\frac{4}{3}$x+8分别交x轴、y轴于A,B两点.线段AB的垂直平分线分别交x轴、y轴于C,D两点.