题目内容
1.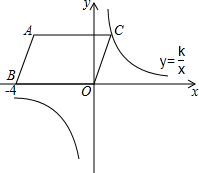 平行四边形ABOC在平面直角坐标系中,A、B的坐标分别为(-3,3),(-4,0).则过C的双曲线表达式为:y=$\frac{3}{x}$
平行四边形ABOC在平面直角坐标系中,A、B的坐标分别为(-3,3),(-4,0).则过C的双曲线表达式为:y=$\frac{3}{x}$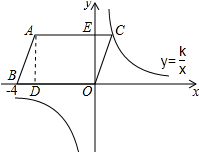 .
.
分析 作AD⊥OB于D,先证明△ABD≌△OCE,得出BD=CE=1,AD=OE=3,得出点C坐标为(1,3),再设过C的双曲线表达式为:y=$\frac{k}{x}$,把点C(1,3)代入求出k即可得出结果.
解答 解:作AD⊥OB于D,如图所示: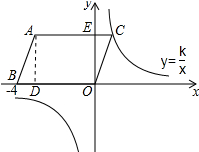 则∠ADB=∠OEC=90°,
则∠ADB=∠OEC=90°,
∵A、B的坐标分别为(-3,3),(-4,0),
∴OB=4,AD=3,OD=3,
∴BD=1,
∵四边形ABOC是平行四边形,
∴∠ABO=∠ACO,AB=OC,
在△ABD和△OCE中,$\left\{\begin{array}{l}{∠ABO=∠OEC}&{\;}\\{∠ABD=∠OCE}&{\;}\\{AB=OC}&{\;}\end{array}\right.$,
∴△ABD≌△OCE(AAS),
∴BD=CE=1,AD=OE=3,
∴C(1,3),
设过C的双曲线表达式为:y=$\frac{k}{x}$,
把点C(1,3)代入得:k=3,
∴y=$\frac{3}{x}$;
故答案为:y=$\frac{3}{x}$.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质、反比例函数图象上点的坐标特征以及解析式的求法;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.-2的相反数的倒数是( )
| A. | 2 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
13.|-2015|的相反数是( )
| A. | 2015 | B. | -2015 | C. | $\frac{1}{2015}$ | D. | -$\frac{1}{2015}$ |
7.小明有一个呈等腰三角形的积木盒,现在积木盒中只剩下如图的九个空格,下面有四种积木的搭配,其中恰好能放入的有( )
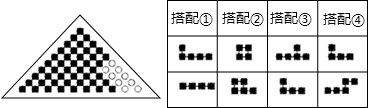

| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
 如图,矩形ABCD中,点E,F分别在AB,CD边上,连接CE、AF,∠DCE=∠BAF.试判断四边形AECF的形状并加以证明.
如图,矩形ABCD中,点E,F分别在AB,CD边上,连接CE、AF,∠DCE=∠BAF.试判断四边形AECF的形状并加以证明.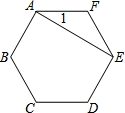 如图,在正六边形ABCDEF中,连接AE,则tan∠1=$\frac{\sqrt{3}}{3}$.
如图,在正六边形ABCDEF中,连接AE,则tan∠1=$\frac{\sqrt{3}}{3}$. 甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.