题目内容
20. 水蜜桃是人们非常喜爱的水果之一,每年七、八月份我市水蜜桃大量上市,今年某水果商以16.5元/千克的价格购进一批水蜜桃进行销售,运输过程中质量损耗5%,运输费用是0.6元/千克,假设不计其他费用.
水蜜桃是人们非常喜爱的水果之一,每年七、八月份我市水蜜桃大量上市,今年某水果商以16.5元/千克的价格购进一批水蜜桃进行销售,运输过程中质量损耗5%,运输费用是0.6元/千克,假设不计其他费用.(1)水果商要把水蜜桃售价至少定为多少才不会亏本?
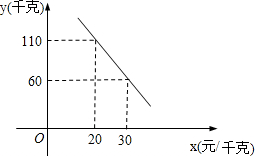
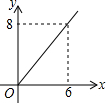
(2)在销售过程中,根据市场调查与预测,水果商发现每天水蜜桃的销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示,那么当销售单价定为多少时,每天获得的利润是640元?
分析 (1)设购进水蜜桃a千克,水蜜桃售价定为m元/千克时,水果商才不会亏本,由题意建立不等式求出其值就可以了;
(2)由(1)可知,每千克水蜜桃的平均成本为18元,再根据售价-进价=利润列出方程,然后解方程即可.
解答 解:(1)设购进水蜜桃a千克,水蜜桃售价定为m元/千克时,水果商才不会亏本,
由题意得:m×a(1-5%)≥a(16.5+0.6),
由 a>0 可解得 m≥18.
答:水果商要把售价至少定为18元/千克才不会亏本;
(2)由(1)可知,每千克水蜜桃的平均成本为18元,
求出y与销售单价x之间的函数关系为y=-5x+210,
由题意得:(x-18)y=(x-18)(-5x+210)=-5x2+300x-3780=640,
解得x=26或34.
答:当销售单价定为26元或34元时,每天获得的利润是640元.
点评 本题考查了一元一次不等式的应用,一次函数的应用,一元二次方程的应用,在解答中求出水蜜桃的平均进价是解题的关键.

练习册系列答案
相关题目
13.|-2015|的相反数是( )
| A. | 2015 | B. | -2015 | C. | $\frac{1}{2015}$ | D. | -$\frac{1}{2015}$ |
12.为了提高节能意识,深圳某中学对全校的耗电情况进行了统计,他们抽查了10天中全校每天的耗电量,数据如下表:(单位:度)
(1)写出学校这10天耗电量的众数和平均数;
(2)若每度电的定价是0.8元,由上题获得的数据,估计该校每月应付电费是多少?(每月按30天计)
(3)如果做到人走电关,学校每天就可节省电量1%,按照每度电0.8元计算,写出该校节省电费y(元)与天数x(取正整数)之间的函数关系式.
| 度数 | 900 | 920 | 950 | 1010 | 1050 | 1100 |
| 天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(2)若每度电的定价是0.8元,由上题获得的数据,估计该校每月应付电费是多少?(每月按30天计)
(3)如果做到人走电关,学校每天就可节省电量1%,按照每度电0.8元计算,写出该校节省电费y(元)与天数x(取正整数)之间的函数关系式.

 甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.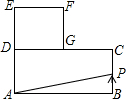 如图,已知长方形ABCD中,AB=4,BC=2,正方形DEFG的边长为2,且点G在CD上,动点P从点B出发,以1个单位长度/s的速度沿折线B→C→G→F向终点F运动,设运动时间为xs,△PAB的面积为y,则y与x之间的函数关系用图象可以表示为( )
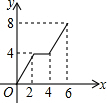
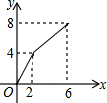
如图,已知长方形ABCD中,AB=4,BC=2,正方形DEFG的边长为2,且点G在CD上,动点P从点B出发,以1个单位长度/s的速度沿折线B→C→G→F向终点F运动,设运动时间为xs,△PAB的面积为y,则y与x之间的函数关系用图象可以表示为( )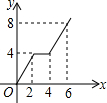
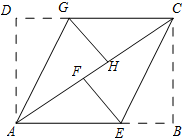 如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的点,E、G分别是折痕CE与AB、AG与CD的交点.
如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的点,E、G分别是折痕CE与AB、AG与CD的交点. 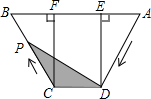 如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,垂足分别为E、F,且AE=EF=FB=5,DE=12,动点P从点C出发,沿C→B→A→D的方向以每秒1个单位长度的速度运动到点D停止,设运动时间为t秒,y=S△CDP,则y与t之间的函数图象大致是( )
如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,垂足分别为E、F,且AE=EF=FB=5,DE=12,动点P从点C出发,沿C→B→A→D的方向以每秒1个单位长度的速度运动到点D停止,设运动时间为t秒,y=S△CDP,则y与t之间的函数图象大致是( )