题目内容
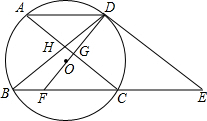 如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F,求证:2AC2=EF•EB.
如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F,求证:2AC2=EF•EB.考点:切线的性质,相似三角形的判定与性质
专题:证明题
分析:用AGD≌△CGF,求出AD=FC,得到FC=CE,再由切线定理求之,化为2AC2=(EC+FC)•EB,得出2AC2=EF•EB.
解答:证明:∵DE为⊙O的切线,
∴DE2=EC•EB,
∵AD∥BC,AC∥DE,
∴四边形ACED是平行四边形,
∴AC=DE,AD=EC,
∴AC2=EC•EB,
又∵OD⊥DE,AC∥DE,
∴FG⊥AC,且AG=CG,
∵AD∥BE,
∴∠ACB=∠CAD,
在△AGD和△CGF中,
∴△AGD≌△CGF(ASA)
∴AD=FC,
∴EC=FC,
∵AC2=EC•EB,
AC2=FC•EB,
∴2AC2=(EC+FC)•EB,
∴2AC2=EF•EB.
∴DE2=EC•EB,
∵AD∥BC,AC∥DE,
∴四边形ACED是平行四边形,
∴AC=DE,AD=EC,
∴AC2=EC•EB,
又∵OD⊥DE,AC∥DE,
∴FG⊥AC,且AG=CG,
∵AD∥BE,
∴∠ACB=∠CAD,
在△AGD和△CGF中,
|
∴△AGD≌△CGF(ASA)
∴AD=FC,
∴EC=FC,
∵AC2=EC•EB,
AC2=FC•EB,
∴2AC2=(EC+FC)•EB,
∴2AC2=EF•EB.
点评:本题主要考查了切线的性质及全等三角形的判定和性质,本题的关键是利用△AGD≌△CGF,求出AD=FC,得到FC=CE,再求证.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知点P(1-2a,a-2)关于原点的对称点在第一象限内,且a为整数,则关于x的分式方程
=2的解是( )
| x+1 |
| x-a |
| A、5 | B、1 | C、3 | D、不能确定 |
 已知,如图,AD⊥DC,AD=4,DC=3,AB=12,问BC的长为多少时,AB⊥AC?证明你的结论.
已知,如图,AD⊥DC,AD=4,DC=3,AB=12,问BC的长为多少时,AB⊥AC?证明你的结论. 如图,AF平分∠BAO,DE平分∠CDO,AF∥DE.AB与CD有怎样的位置关系?为什么?
如图,AF平分∠BAO,DE平分∠CDO,AF∥DE.AB与CD有怎样的位置关系?为什么?
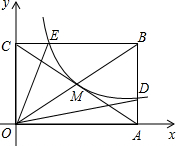 如图,反比例函数y=
如图,反比例函数y=