题目内容
计算下列各题
(1)(5m3n2)2•(-2m2)3•(-n3)4
(2)(3a2b)3•(-2ab4)2÷(6a5b3)
(3)x (x-y)-(x-3)(x+3)
(4)(3x+2)(3x-2)-5x (x-1)-(2x-1)2
(5)(a+b)2-(a-b)2
(6)(a-2b+3c) (a+2b-3c)
(7)(
x+
y)(
x-
y)-(
x-
y)2
(8)[2x2-(x+y)(x-y)][(-x-y)(-x+y)+2y2],其中x=-1,y=-2.
(1)(5m3n2)2•(-2m2)3•(-n3)4
(2)(3a2b)3•(-2ab4)2÷(6a5b3)
(3)x (x-y)-(x-3)(x+3)
(4)(3x+2)(3x-2)-5x (x-1)-(2x-1)2
(5)(a+b)2-(a-b)2
(6)(a-2b+3c) (a+2b-3c)
(7)(
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 3 |
| 3 |
| 4 |
(8)[2x2-(x+y)(x-y)][(-x-y)(-x+y)+2y2],其中x=-1,y=-2.
考点:整式的混合运算,整式的混合运算—化简求值
专题:计算题
分析:(1)原式利用幂的乘方与积的乘方运算法则计算,合并即可得到结果;
(2)原式利用幂的乘方与积的乘方运算法则计算,再利用单项式乘除单项式法则计算即可得到结果;
(3)原式利用单项式乘以多项式,以及多项式乘以多项式法则计算,去括号合并即可得到结果;
(4)原式第一项利用平方差公式计算,第二项利用单项式乘以多项式法则计算,最后一项利用完全平方公式展开,去括号合并即可得到结果;
(5)原式利用完全平方公式展开,去括号合并即可得到结果;
(6)原式先利用平方差公式计算,再利用完全平方公式展开即可得到结果;
(7)原式第一项利用平方差函数化简,第二项利用完全平方公式展开,去括号合并即可得到结果;
(8)原式中括号中利用平方差公式化简,整理后再利用多项式乘以多项式法则计算,得到最简结果,将x与y的值代入计算即可求出值.
(2)原式利用幂的乘方与积的乘方运算法则计算,再利用单项式乘除单项式法则计算即可得到结果;
(3)原式利用单项式乘以多项式,以及多项式乘以多项式法则计算,去括号合并即可得到结果;
(4)原式第一项利用平方差公式计算,第二项利用单项式乘以多项式法则计算,最后一项利用完全平方公式展开,去括号合并即可得到结果;
(5)原式利用完全平方公式展开,去括号合并即可得到结果;
(6)原式先利用平方差公式计算,再利用完全平方公式展开即可得到结果;
(7)原式第一项利用平方差函数化简,第二项利用完全平方公式展开,去括号合并即可得到结果;
(8)原式中括号中利用平方差公式化简,整理后再利用多项式乘以多项式法则计算,得到最简结果,将x与y的值代入计算即可求出值.
解答:解:(1)原式=25m6n4•(-8m6)÷n12=-
;
(2)原式=(27a6b3)•(4a2b8)÷(6a5b3)=18a3b8;
(3)原式=x2-xy-x2+9=9-xy;
(4)原式=9x2-4-5x2+5x-4x2+4x-1=9x-5;
(5)原式=a2+2ab+b2-a2+2ab-b2=4ab;
(6)原式=a2-(2b-3c)2=a2-4b2+12bc-9c2;
(7)原式=
x2-
y2-
x2+
xy-
y2=-
y2+
xy;
(8)原式=(2x2-x2+y2)(x2-y2+2y2)=x4+2x2y2+y4.
| 200m12 |
| n8 |
(2)原式=(27a6b3)•(4a2b8)÷(6a5b3)=18a3b8;
(3)原式=x2-xy-x2+9=9-xy;
(4)原式=9x2-4-5x2+5x-4x2+4x-1=9x-5;
(5)原式=a2+2ab+b2-a2+2ab-b2=4ab;
(6)原式=a2-(2b-3c)2=a2-4b2+12bc-9c2;
(7)原式=
| 1 |
| 9 |
| 9 |
| 16 |
| 1 |
| 9 |
| 1 |
| 2 |
| 9 |
| 16 |
| 9 |
| 8 |
| 1 |
| 2 |
(8)原式=(2x2-x2+y2)(x2-y2+2y2)=x4+2x2y2+y4.
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
9的相反数是( )
| A、-9 | ||
| B、9 | ||
| C、±9 | ||
D、
|
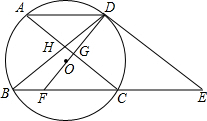 如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F,求证:2AC2=EF•EB.
如图,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC、BC于点G、F,求证:2AC2=EF•EB.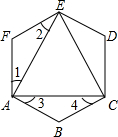 如图,已知六边形ABCDEF的内角都相等,且∠1=∠2,∠3=∠4.求∠CAE的度数.
如图,已知六边形ABCDEF的内角都相等,且∠1=∠2,∠3=∠4.求∠CAE的度数.