题目内容
5.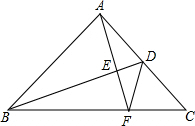 如图,BD是等腰直角△ABC的腰AC上的中线,AE⊥BD交BD、BC于E、F,
如图,BD是等腰直角△ABC的腰AC上的中线,AE⊥BD交BD、BC于E、F,求证:(1)∠ABD=∠CAF;
(2)∠ADB=∠CDF.
分析 (1)由∠BAC为直角,得到其他两锐角互余,又根据AE与BD垂直,得到三角形ADF为直角三角形,故两锐角也互余,根据同角的余角相等即可得证;
(2)过A、D分别做BC的垂线,设AG的长为1,得出与之相关联的线段的长度,进而利用角的正切值相等得出∠DBH=∠FDH,即可得出结论.
解答 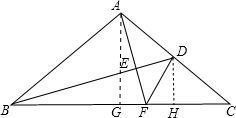 证明:(1)∵∠BAC=90°,
证明:(1)∵∠BAC=90°,
∴∠ABD+∠ADF=90°,
又AE⊥BD,∴∠AFD=90°,
∴∠DAF+∠ADF=90°,
∴∠ABD=∠CAF;
(2)过A、D分别做BC的垂线,垂足分别为G、H.
设AG=1,那么CG=1,DH=$\frac{1}{2}$,BH=$\frac{2}{3}$,
tan∠DBH=$\frac{1}{3}$,
又∵∠GAF=∠DBH,
∴GF=$\frac{1}{3}$AG=$\frac{1}{3}$,
FH=GH-GF=$\frac{1}{2}$-$\frac{1}{3}$=$\frac{1}{6}$,
tan∠FDH=$\frac{FH}{DH}$=$\frac{1}{3}$,
∴∠DBH=∠FDH
∵∠ADB=∠DBH+∠C,
∠CDF=∠FDH+∠CDH,
∴∠ADB=∠CDF
点评 本题主要考查了全等三角形的判定与性质,等腰三角形的性质以及由正切值判定两个角相等,无论是证明还是计算题,都应该从不同角度思考,利用已学知识熟练求解.

练习册系列答案
相关题目
8.用长100cm的金属丝围成一个矩形框子,框子的面积不可能是( )
| A. | 375cm2 | B. | 500cm2 | C. | 625cm2 | D. | 700cm2 |
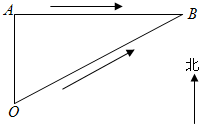 如图,某海关缉私艇在点0处发现在正北方向30海里的A处有一艘可疑船只,测得它正以60海里∕时的速度向正东方航行,随即调整方向,以75海里∕时的速度准备在B处迎头拦截.问经过多少时间能赶上?
如图,某海关缉私艇在点0处发现在正北方向30海里的A处有一艘可疑船只,测得它正以60海里∕时的速度向正东方航行,随即调整方向,以75海里∕时的速度准备在B处迎头拦截.问经过多少时间能赶上?