题目内容
14．已知直角三角形的一条直角边的长是另一条直角边的长的2倍，斜边长为10$\sqrt{5}$，求较短的直角边的长．分析 根据边之间的关系，运用勾股定理，列方程解答即可．
解答 解：设较短的直角一边是x，另一直角边是2x，
根据勾股定理得到方程x2+（2x）2=（10$\sqrt{5}$）2，
解得：x=10（其中x=-10不合题意舍去）．
故较短的直角边的长是10．
点评 本题考查了一元二次方程和勾股定理的应用，解题的关键是根据勾股定理得到方程，转化为方程问题．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
如图，△ABC中，DB平分∠ABC，DC平分△ABC的外角∠ACE，∠D=m°，求∠A的度数．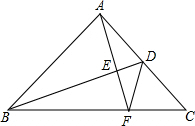
如图，BD是等腰直角△ABC的腰AC上的中线，AE⊥BD交BD、BC于E、F，
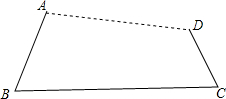如图，用钉子把木棒AB、BC和CD分别在端点B、C处连接起来，用橡皮筋把AD连接起来