题目内容
7.已知:二次函数y1=a(x+1)2的图象与一次函数y2=kx+k的图象有一个公共点是(1,2).(1)求二次函数及一次函数解析式;
(2)求出另一个交点坐标;
(3)在同一坐标系中画出它们的图形,说明x取何值时,y1=y2,y1<y2,y1>y2.
分析 (1)分别把(1,2)代入一次函数和反比例函数解析式求出a和k即可;
(2)两个解析式联立方程,解方程即可求得;
(3)画出图象,根据图象即可求得.
解答 解:(1)将(1,2)代入二次函数y1=a(x+1)2得:4a=2,即a=$\frac{1}{2}$,
将(1,2)代入一次函数解析式得:k+k=2,即k=1,
∴二次函数解析式为y1=$\frac{1}{2}$(x+1)2,一次函数解析式为y2=x+1;
(2)解$\left\{\begin{array}{l}{y=\frac{1}{2}(x+1)^{2}}\\{y=x+1}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$,
∴二次函数y1=a(x+1)2的图象与一次函数y2=kx+k的图象的另一个交点是(-1,0);
(3)画出图象如图所示: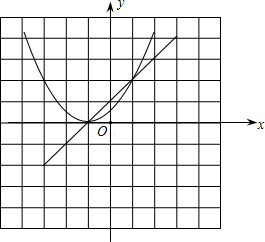
由图象可知:当x=-1或x=1时,y1=y2;
当-1<x<1时,y1<y2;
当x<-1或x>1时,y1>y2.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式以及函数与不等式的关系.

练习册系列答案
相关题目
17.现有一个圆心角为120°,半径为6的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),该圆锥底面圆的半径为( )
| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1cm |
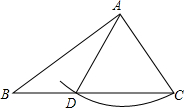 学习了全等三角形后,同学们都知道存在“边角边”的判定方怯.接着同学们探究是否存在“边边角”的判定方法,即“有两边和其中一边的对角对应相等的两个三角形全等”这个命题是真命题还是假命题.
学习了全等三角形后,同学们都知道存在“边角边”的判定方怯.接着同学们探究是否存在“边边角”的判定方法,即“有两边和其中一边的对角对应相等的两个三角形全等”这个命题是真命题还是假命题.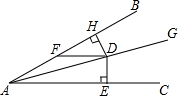 如图所示.已知∠BAC=30°,AD平分∠BAC.DE⊥AC于点E.DH⊥AB于点H,DF∥AC,交AB于点F.若DF=10cm.求DE的长.
如图所示.已知∠BAC=30°,AD平分∠BAC.DE⊥AC于点E.DH⊥AB于点H,DF∥AC,交AB于点F.若DF=10cm.求DE的长.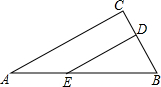 如图,在Rt△ABC中,∠C=90°,ED⊥BC,D为垂足,BD=3cm,DC=2cm,AB=6cm.求BE和EA的长.
如图,在Rt△ABC中,∠C=90°,ED⊥BC,D为垂足,BD=3cm,DC=2cm,AB=6cm.求BE和EA的长. ”表示a-b+c,“
”表示a-b+c,“ ”表示x-y+z-w,求
”表示x-y+z-w,求 +
+ 的值.
的值. 如图,△ABC中,DB平分∠ABC,DC平分△ABC的外角∠ACE,∠D=m°,求∠A的度数.
如图,△ABC中,DB平分∠ABC,DC平分△ABC的外角∠ACE,∠D=m°,求∠A的度数.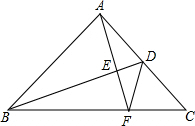 如图,BD是等腰直角△ABC的腰AC上的中线,AE⊥BD交BD、BC于E、F,
如图,BD是等腰直角△ABC的腰AC上的中线,AE⊥BD交BD、BC于E、F,