题目内容
12.已知三角形的两边长是方程x2-2$\sqrt{3}$x+1=0的两根.则三角形的第三边c的取值范围是2$\sqrt{2}$<c<2$\sqrt{3}$.分析 设方程x2-2$\sqrt{3}$x+1=0的两根为a和b,根据根与系数的关系得到a+b=2$\sqrt{3}$,ab=1,再利用完全平方根是得到|a-b|=$\sqrt{(a+b)^{2}-4ab}$,则可计算出|a-b|=2$\sqrt{2}$,然后根据三角形三边的关系可确定c的取值范围.
解答 解:设方程x2-2$\sqrt{3}$x+1=0的两根为a和b,
根据题意得a+b=2$\sqrt{3}$,ab=1,
所以|a-b|=$\sqrt{(a-b)^{2}}$=$\sqrt{(a+b)^{2}-4ab}$=$\sqrt{(2\sqrt{3})^{2}-4×1}$=2$\sqrt{2}$,
所以2$\sqrt{2}$<c<2$\sqrt{3}$.
故答案为2$\sqrt{2}$<c<2$\sqrt{3}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了三角形三边的关系.

练习册系列答案
相关题目
12.下列说法中,正确的是( )
| A. | 一组邻边相等的四边形是菱形 | |
| B. | 对角线相等的平行四边形是菱形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线交点到各边距离相等的四边形是菱形 |
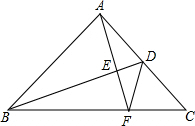 如图,BD是等腰直角△ABC的腰AC上的中线,AE⊥BD交BD、BC于E、F,
如图,BD是等腰直角△ABC的腰AC上的中线,AE⊥BD交BD、BC于E、F,