题目内容
17.如图①,把一个直角三角尺XYZ放置在△ABC上,恰好三角尺XYZ上两条直角边XY,XZ分别经过点B,C,若∠A=30°.则∠ABC+∠ACB=150°,则∠ABX+∠ACX=60°;如图②,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的度数.
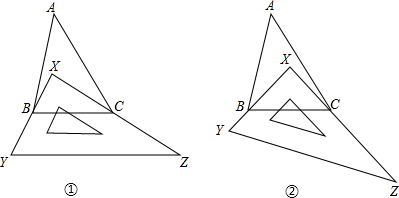
分析 (1)在△ABC中,利用三角形内角和等于180°,可求∠ABC+∠ACB=180°-∠A,即可求∠ABC+∠ACB;根据∠ABC+∠ACB=150°,∠XBC+∠XCB=90°,即可求出答案;
(2)不发生变化,由于在△ABC中,∠A=30°,从而∠ABC+∠ACB是一个定值,即等于150°,同理在△XBC中,∠BXC=90°,那么∠XBC+∠XCB也是一个定值,等于90°,于是∠ABX+∠ACX的值不变,等于150°-90°=60°.
解答 解:(1)∵∠A=30°,
∴∠ABC+∠ACB=150°,
∵∠X=90°,
∴∠XBC+∠XCB=90°,
∴∠ABC+∠ACB=150°;
∵在△BCX中,∠BXC=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=150°-90°=60°;
故答案为:150,60;
(2)不变化.
∵∠A=30°,
∴∠ABC+∠ACB=150°,
∵∠X=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=(∠ABC-∠XBC)+(∠ACB-∠XCB)
=(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.
点评 此题主要考查了三角形内角和定理,此题注意运用整体法计算,关键是求出∠ABC+∠ACB.

练习册系列答案
相关题目
12.下列说法中,正确的是( )
| A. | 一组邻边相等的四边形是菱形 | |
| B. | 对角线相等的平行四边形是菱形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线交点到各边距离相等的四边形是菱形 |
 ”表示a-b+c,“
”表示a-b+c,“ ”表示x-y+z-w,求
”表示x-y+z-w,求 +
+ 的值.
的值.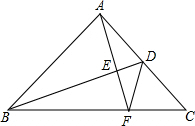 如图,BD是等腰直角△ABC的腰AC上的中线,AE⊥BD交BD、BC于E、F,
如图,BD是等腰直角△ABC的腰AC上的中线,AE⊥BD交BD、BC于E、F,
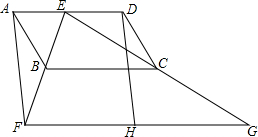 如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.