题目内容
14.已知a、b、c为△ABC三条边的长.(1)当b2+2ab=c2+2ac时,判断△ABC的形状;
(2)求证:a2-b2-c2-2bc<0.
分析 (1)把b2+2ab=c2+2ac进行因式分解,即可解答;
(2)将不等式的左边因式分解后根据三角形三边关系判断代数式的符号即可.
解答 解:(1)b2+2ab=c2+2ac
b2+2ab-c2-2ac=0
(b2-c2)+(2ab-2ac)=0
(b+c)(b-c)+2a(b-c)=0
(b-c)(b+c+2a)=0,
∵b+c+2a≠0,
∴b-c=0,
∴b=c,
∴△ABC为等腰三角形.
(2)a2-b2-c2-2bc
=a2-(b2+c2+2bc)
=a2-(b+c)2
=(a+b+c)(a-b-c),
∵a、b、c为△ABC三条边的长.
∴a+b+c>0,a-b-c<0,
∴a2-b2-c2-2bc<0.
点评 本题考查了因式分解的应用,解决本题的关键是把多项式进行分解因式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
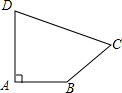 如图所示的四边形ABCD中,其中AB=3,BC=12,CD=13,DA=4,∠A=90°,你能求出四边形ABCD的面积吗?
如图所示的四边形ABCD中,其中AB=3,BC=12,CD=13,DA=4,∠A=90°,你能求出四边形ABCD的面积吗?