题目内容
4.实数a满足($\sqrt{a-1}$)2+$\sqrt{(1-a)^{2}}$=4,求a的值.分析 利用平方根定义及二次根式性质求出a的值即可.
解答 解:已知等式整理得:a-1+a-1=4,
解得:a=3.
点评 此题考查了二次根式的性质与化简,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12.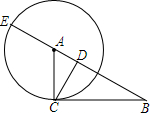 在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )
在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )
 在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )
在Rt△ABC中,∠BCA=90°,以A为圆心,AC为半径的圆交AB于F,交BA延长线于E,CD⊥AB于D,给出四个等式①BC2=BF•BA;②CD2=AD•AB;③CD2=DF•DE;④BF•BE=BD•BA,其中能够成立的是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.下列各数中,属于无理数的是( )
| A. | $\root{3}{8}$ | B. | $\sqrt{8}$ | C. | $\frac{22}{7}$ | D. | 3.1415926 |
10.当1<a<2时,式子$\sqrt{(a-2)^{2}}$+|1-a|的值为( )
| A. | 3-2a | B. | 2a-3 | C. | -1 | D. | 1 |
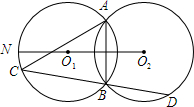 已知:两等圆⊙O1与⊙O2相交于点A、B,若点O1在⊙O2外,延长O2O1交⊙O1于点N,在劣弧$\widehat{NB}$上任取一点C(点C与点B不重合),CB的延长线交⊙O2于点D,如图所示,连结AC,试比较AC与AB的大小.
已知:两等圆⊙O1与⊙O2相交于点A、B,若点O1在⊙O2外,延长O2O1交⊙O1于点N,在劣弧$\widehat{NB}$上任取一点C(点C与点B不重合),CB的延长线交⊙O2于点D,如图所示,连结AC,试比较AC与AB的大小.