题目内容
5．
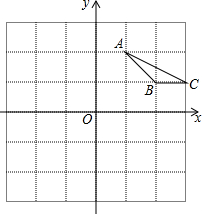如图，平面直角坐标系中，△ABC的顶点在方格纸的格点处，每个小正方形的边长为单位1．（1）请作出△ABC向左平移三个单位后得到的图形△A1B1C1；
（2）请作出△ABC绕点O顺时针旋转90度后得到的图形△A2B2C2；
（3）在坐标轴上找到一点D，使△ABD是以AB为腰的等腰三角形，并写出点D的坐标．
分析 （1）利用平移的性质写出点A、B、C的对应点A1、B1、C1的坐标，然后描点即可得到△A1B1C1；
（2）利用网格特点和旋转的性质画出点A、B、C的对应点A2、B2、C2的坐标，从而得到△A2B2C2；
（3）分别以A、B为圆心，AB为半径画弧与坐标轴相交，则交点D可满足△ABD是以AB为腰的等腰三角形，再写出D点坐标．
解答 解：（1）如图1，△A1B1C1为所作；
（2）如图1，△A2B2C2为所作；
（3）如图2，点D和点D′为所作，点D的坐标为（0，1）或（1，0）．
点评 本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了平移变换和等腰三角形的性质．
练习册系列答案
相关题目
15．计算：$\frac{12}{{m}^{2}-9}+\frac{2}{3-m}$=（ ）
| A． | -$\frac{2}{m+3}$ | B． | $\frac{2}{m+3}$ | C． | -$\frac{2}{m-3}$ | D． | $\frac{2}{m-3}$ |
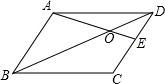如图，在?ABCD中，E为CD中点，AE交BD于点O，S△AOB=12cm2，则S△EOD=3cm2．
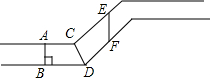一条公路的段如图所示，图中哪条线段的长度能比较确切地描述这一段公路的宽度？请说明理由．