��Ŀ����
10����֪��$\frac{1}{1��2}$=1-$\frac{1}{2}$��$\frac{1}{2��3}$=$\frac{1}{2}-\frac{1}{3}$��$\frac{1}{3��4}$=$\frac{1}{3}-\frac{1}{4}$��$\frac{1}{4��5}$=$\frac{1}{4}$-$\frac{1}{5}$������1����գ�$\frac{1}{2}$+$\frac{1}{2��3}$+$\frac{1}{3��4}$+��+$\frac{1}{n��n+1��}$=$\frac{n}{n+1}$��
��2�������㷢�ֵĹ��ɽⷽ�̣�
$\frac{1}{��x+2����x+3��}$+$\frac{1}{��x+3����x+4��}$+$\frac{1}{��x+4����x+5��}$+��+$\frac{1}{��x+2013����x+2014��}$=$\frac{x}{��x+2����x+2014��}$��
���� ��1�������ܽ�õ�������ɣ���ԭʽ���κ���㼴�ɵõ������
��2�����õó��IJ�����ɽ����̱��Σ�����⣬���鼴�ɣ�
��� �⣺��1��ԭʽ=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+��+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$��
��2�����������ã�$\frac{1}{x+2}$-$\frac{1}{x+3}$+$\frac{1}{x+3}$-$\frac{1}{x+4}$+��+$\frac{1}{x+2013}$-$\frac{1}{x+2014}$=$\frac{x}{��x+2����x+2014��}$��
��$\frac{2012}{��x+2����x+2014��}$=$\frac{x}{��x+2����x+2014��}$��
ȥ��ĸ�ã�x=2012��
������x=2012�Ƿ�ʽ���̵Ľ⣮
�ʴ�Ϊ����1��$\frac{n}{n+1}$
���� ���⿼���˽��ʽ���̣����ʽ���̵Ļ���˼���ǡ�ת��˼�롱���ѷ�ʽ����ת��Ϊ��ʽ������⣮���ʽ����һ��ע��Ҫ�����

��ϰ��ϵ�д�
�����Ŀ
18�� ��ͼ���ڡ�ABC�У�BC=5��AC=8��AB�Ĵ�ֱƽ���߽�AB�ڵ�D����AC�ڵ�E�����BCE���ܳ����ڣ�������
��ͼ���ڡ�ABC�У�BC=5��AC=8��AB�Ĵ�ֱƽ���߽�AB�ڵ�D����AC�ڵ�E�����BCE���ܳ����ڣ�������
 ��ͼ���ڡ�ABC�У�BC=5��AC=8��AB�Ĵ�ֱƽ���߽�AB�ڵ�D����AC�ڵ�E�����BCE���ܳ����ڣ�������
��ͼ���ڡ�ABC�У�BC=5��AC=8��AB�Ĵ�ֱƽ���߽�AB�ڵ�D����AC�ڵ�E�����BCE���ܳ����ڣ�������| A�� | 18 | B�� | 15 | C�� | 13 | D�� | 12 |
15�����x2+xy=3��y2+xy=-2����ôx2+3xy+2y2=��������
| A�� | -1 | B�� | 1 | C�� | 2 | D�� | 3 |
 ��ͼ����10��6�������У�ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ����Ϊ��㣬��AOB�Ķ��㶼�ڸ���ϣ���O����ֱ������ϵ��ԭ�㣮
��ͼ����10��6�������У�ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ����Ϊ��㣬��AOB�Ķ��㶼�ڸ���ϣ���O����ֱ������ϵ��ԭ�㣮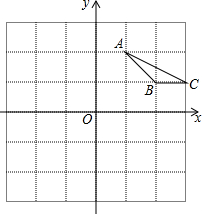 ��ͼ��ƽ��ֱ������ϵ�У���ABC�Ķ����ڷ���ֽ�ĸ�㴦��ÿ��С�����εı߳�Ϊ��λ1��
��ͼ��ƽ��ֱ������ϵ�У���ABC�Ķ����ڷ���ֽ�ĸ�㴦��ÿ��С�����εı߳�Ϊ��λ1��