题目内容
14.下列一元二次方程有两个相等实数根的是( )| A. | x2+4=0 | B. | x2-2x=0 | C. | (x+1)2=0 | D. | (x-3)(x+1)=0 |
分析 通过根的判别式来判断A、B两个选项中方程根的情况,通过解方程来判断C、D两个选项中方程根的情况,由此即可得出结论.
解答 解:A、x2+4=0,
∵△=0-4×1×4=-16<0,
∴该方程无实数根;
B、x2-2x=0,
∵△=(-2)2-4×1×0=4>0,
∴该方程有两个不等的实数根;
C、(x+1)2=0,即x+1=0,
解得:x=-1,
∴该方程有两个相等的实数根;
D、(x-3)(x+1)=0,
解得:x=3或x=-1,
∴该方程有两个不等的实数根.
故选C.
点评 本题考查了根的判别式以及解一元二次方程,解题的关键是分析四个选项中方程根得情况.本题属于基础题,难度不大,解决该题型题目时,根据根的判别式的符号得出根的个数是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.a、b、c为△ABC三边,不是直角三角形的是( )
| A. | a2=c2-b2 | B. | a=6,b=10,c=8 | ||
| C. | ∠A:∠B:∠C=3:4:5 | D. | a=8k,b=17k,c=15k |
9.下列关于$\sqrt{8}$的说法中,错误的是( )
| A. | $\sqrt{8}$是8的算术平方根 | B. | 2<$\sqrt{8}$<3 | ||
| C. | $\sqrt{8}$=$±2\sqrt{2}$ | D. | $\sqrt{8}$是无理数 |
6.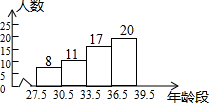 菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )
菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )
 菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )
菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )| A. | 平均年龄是37.5岁 | B. | 中位数年龄位于33.5-36.5岁 | ||
| C. | 众数年龄位于36.5-39.5岁 | D. | 以上选项都不正确 |
3.实数$\sqrt{5}$的值在( )
| A. | 0与1之间 | B. | 1与2之间 | C. | 2与3之间 | D. | 3与4之间 |
 如图(1),AB∥CD,猜想∠BPD与∠B、∠D的数量关系,并说明理由.
如图(1),AB∥CD,猜想∠BPD与∠B、∠D的数量关系,并说明理由. 双休日,小明在公园放风筝,如图,拿风筝线的手A离地面高度AE为1.5米,风筝飞到C处时的线长AC为30米,这时测得∠CAB=60°
双休日,小明在公园放风筝,如图,拿风筝线的手A离地面高度AE为1.5米,风筝飞到C处时的线长AC为30米,这时测得∠CAB=60°