题目内容
19. 双休日,小明在公园放风筝,如图,拿风筝线的手A离地面高度AE为1.5米,风筝飞到C处时的线长AC为30米,这时测得∠CAB=60°
双休日,小明在公园放风筝,如图,拿风筝线的手A离地面高度AE为1.5米,风筝飞到C处时的线长AC为30米,这时测得∠CAB=60°(1)求此时风筝离地面的高度(结果精确到0.1米,$\sqrt{3}$≈1.73);
(2)若小明的风筝线最长能放出35米,则小明站在原地不动时,风筝能否向右水平漂移到点F,使∠FAB=45°?若能,求出风筝水平漂移的距离;若不能,说明理由.
分析 (1)在Rt△ABC中,由三角函数求出BC的长度,得出CD即可;
(2)作FM⊥AB于M,则FM=BC=15$\sqrt{3}$米,在Rt△AMF中,AF=35米,由三角函数得出∠FAB>45°即可.
解答 解:(1)在Rt△ABC中,∠CAB=60°,
∴BC=AC•sin60°=30×$\frac{\sqrt{3}}{2}$=15$\sqrt{3}$≈15×1.73=25.95(米),
∴CD=BC+BD=25.95+1.5≈27.5(米);.
答:此时风筝离地面的高度约为27.5米;
(2)不能使∠FAB=45°;理由如下:
作FM⊥AB于M,如图所示:
则FM=BC=15$\sqrt{3}$米,
在Rt△AMF中,AF=35米,sin∠FAB=$\frac{FM}{AF}$=$\frac{15\sqrt{3}}{35}$≈0.7414>$\frac{\sqrt{2}}{2}$,
∴∠FAB>45°,
即小明站在原地不动时,风筝不能向右水平漂移到点F,使∠FAB=45°.
点评 本题考查了解直角三角形的应用、三角函数;由三角函数求出BC是解决问题的关键.

练习册系列答案
相关题目
14.下列一元二次方程有两个相等实数根的是( )
| A. | x2+4=0 | B. | x2-2x=0 | C. | (x+1)2=0 | D. | (x-3)(x+1)=0 |
7. 有理数a,b在数轴上对应位置如图所示,则a-b的值为( )
有理数a,b在数轴上对应位置如图所示,则a-b的值为( )
 有理数a,b在数轴上对应位置如图所示,则a-b的值为( )
有理数a,b在数轴上对应位置如图所示,则a-b的值为( )| A. | 大于0 | B. | 小于0 | C. | 等于0 | D. | 大于a |

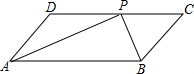 如图,在?ABCD中,∠ABC与∠BAD的平分线交于点P,且点P在CD边上.
如图,在?ABCD中,∠ABC与∠BAD的平分线交于点P,且点P在CD边上.