先化简.再求$\frac{{x}^{2}-1}{{x}^{2}+x}$÷(2-$\frac{{x}^{2}+1}{x}$)的值.其中x=-2cos60°+3tan45°．题目和参考答案——青夏教育精英家教网—

题目内容

19．先化简，再求$\frac{{x}^{2}-1}{{x}^{2}+x}$÷（2-$\frac{{x}^{2}+1}{x}$）的值，其中x=-2cos60°+3tan45°．

分析原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，求出x的值代入计算即可求出值．

解答解：原式=$\frac{（x+1）（x-1）}{x（x+1）}$÷$\frac{2x-{x}^{2}-1}{x}$
=$\frac{x-1}{x}$•$\frac{x}{-（x-1）^{2}}$
=-$\frac{1}{x-1}$，
当x=-2cos60°+3tan45°=-1+3=2时，原式=-1．

点评此题考查了分式的化简求值，以及特殊角的三角函数值，熟练掌握运算法则是解本题的关键．

练习册系列答案

相关题目

9．根据下列表述，能确定具体位置的是（　　）

	A．	奥斯卡影院2号厅3排		B．	汝南县汝宁大街
	C．	东经118°		D．	天中山北偏东60°，10km处

10．在平面直角坐标系中，点P的坐标为（3，-1），那么点P在（　　）

7．如图，抛物线y=-$\frac{1}{2}$x²+mx+n与x轴交于A，B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，顶点为P点，已知A（-1，0），B（4，0）．
（1）求抛物线的表达式；
（2）试判断以点P为圆心，PC为半径的圆与直线CD的位置关系并说明理由；
（3）点E是线段BC上的一动点．
①是否存在这样的点E，使△ECD是等腰三角形，如果存在，直接写出E点的坐标，如果不存在，请说明理由；
②过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．

14．下列一元二次方程有两个相等实数根的是（　　）

a⁶÷a³=a²

（a³）²=a⁵

11．计算：
（1）$\frac{1}{x-3}$-$\frac{3}{x（x-3）}$
（2）（$\frac{m}{m+3}$-$\frac{2m}{m+3}$）÷$\frac{m}{{m}^{2}-9}$
（3）|-2|+（$\frac{1}{3}$）²+（π-2）⁰-$\sqrt{9}$．

8．

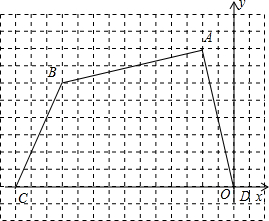如图，四边形ABCD各个顶点的坐标分别为（-2，8），（-11，6），（-14，0），（0，0）．
（1）求这个四边形的面积．
（2）如果把原来的四边形ABCD向下平移3个单位长度，再向左平移2个单位长度后得到新的四边形A₁B₂C₃D₄，请直接写出平移后的四边形各点的坐标和新四边形的面积．

4．如图，点A、点B在数轴上表示的数分别是-4和4．若在数轴上存在一点P到A的距离是点P到B的距离的3倍，则点P所表示的数是2或8．

试题分类