题目内容
16.在直角坐标系xOy中,点P(4,y)在第四象限内,且OP与x轴正半轴的夹角的正切值是2,则y的值是-8.分析 根据题意得到OA=4,又因为OP与x轴正半轴的夹角的正切值是2,所以tan∠AOP=2,然后利用三角函数的定义即可求解.
解答 解:如图,
∵点P(4,y)在第四象限内,
∴OA=4,PA=-y
又∵OP与x轴正半轴的夹角的正切值是2,
∴tan∠AOP=2,
∴$\frac{PA}{OA}$=2,
∴-y=2×4,
∴y=-8,
故答案为:-8.
点评 此题主要考查了三角函数的定义,也考查了数形结合的思想,解题时首先利用数形结合的思想利用坐标表示线段的长度,然后利用三角函数的定义列出方程即可解决问题.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
11.在方程组$\left\{\begin{array}{l}{x+2y=4k}\\{2x+y=2k+1}\end{array}\right.$中,若未知数x、y满足x-y>0,则k的取值范围是( )
| A. | k$>\frac{1}{2}$ | B. | k$<\frac{1}{2}$ | C. | k$>-\frac{1}{2}$ | D. | k$<-\frac{1}{2}$ |
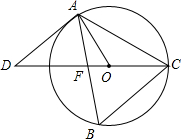 如图,△ABC内接于⊙O,∠B=66°,CE是⊙O的直径,点D是CE延长线上的一点.且∠D=42°.
如图,△ABC内接于⊙O,∠B=66°,CE是⊙O的直径,点D是CE延长线上的一点.且∠D=42°.