题目内容
11.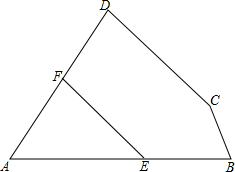 如图,E,F是四边形ABCD的边AB,AD上的两点,若∠B+∠C+∠D-∠BEF-∠DFE=60°,求∠A的度数.
如图,E,F是四边形ABCD的边AB,AD上的两点,若∠B+∠C+∠D-∠BEF-∠DFE=60°,求∠A的度数.
分析 根据内角与相邻的外角互补,可得∠AEE与∠AEF,根据三角形的内角和,四边形的内角,可得关于∠A的方程,根据解方程,可得答案.
解答 解:由内角与相邻的外角互补,得
∠DFE=180°-∠AFE,∠BEF=180-∠AEF.
由等量代换,得
∠B+∠C+∠D-(180°-∠AFF)-(180°-∠AEF)=60.
∠B+∠C+∠D-180°+∠AFE-180°+∠AEF=60°.
由内角和定理,得
360°-∠A-180°-180°+(180°-∠A)=60°.
解得∠A=60°
点评 本题考查了多边形的内角与外角,利用多边形的内角和定理得出关于∠A的方程是解题关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
19.若$\root{3}{x}$+$\root{3}{y}$=0,则x与y的关系是( )
| A. | x+y≠0 | B. | x=y | C. | x+y=0 | D. | x=$\frac{1}{y}$ |
3.下列说法正确的是( )
| A. | 一组对边相等且平行的四边形是平行四边形 | |
| B. | 有两边相等的四边形是平行四边形 | |
| C. | 四个全等的三角形一定可组成一个平行四边形 | |
| D. | 一组对边平行,另一组对边相等的四边形是平行四边形 |
20.若x=2m+1,y=3+4m,则用含x的代数式表示y为( )
| A. | 3+$\frac{x}{2}$ | B. | 3+x2 | C. | 3+$\frac{{x}^{2}}{4}$ | D. | 3+4x2 |
5.如果10b=n,那么称b为n的劳格数,记为b=d(n),如102=100,则2=d(100);104=10000,则4=d(10000).由定义可知:10b=n与b=d(n)所表示的是b,n两个量之间的同一关系.
(1)根据劳格数的定义,填空:d(10)=1,d(103)=3;
(2)劳格数有如下运算性质:若m,n为正数,则d(mn)=d(m)+d(n),d($\frac{m}{n}$)=d(m)-d(n).
根据运算性质填空,填空:若d(2)=0.3010,则d(4)=0.6020;d(5)=0.6990;d(0.08)=-1.0970.
(3)下表中与数x对应的劳格数d(x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
(1)根据劳格数的定义,填空:d(10)=1,d(103)=3;
(2)劳格数有如下运算性质:若m,n为正数,则d(mn)=d(m)+d(n),d($\frac{m}{n}$)=d(m)-d(n).
根据运算性质填空,填空:若d(2)=0.3010,则d(4)=0.6020;d(5)=0.6990;d(0.08)=-1.0970.
(3)下表中与数x对应的劳格数d(x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| d(x) | 3a-b+c | 2a-b | a+c | 1+a-b-c | 3-3a-3c | 4a-2b | 3-b-2c | 6a-3b |
 如图,已知:a∥b,三角板的直角顶点在直线b上,∠1=40°,则∠2=50°.
如图,已知:a∥b,三角板的直角顶点在直线b上,∠1=40°,则∠2=50°.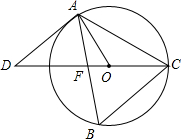 如图,△ABC内接于⊙O,∠B=66°,CE是⊙O的直径,点D是CE延长线上的一点.且∠D=42°.
如图,△ABC内接于⊙O,∠B=66°,CE是⊙O的直径,点D是CE延长线上的一点.且∠D=42°.