题目内容
9.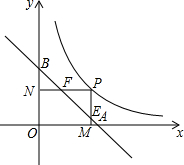 如图,A、B分别是x、y轴上的点,且OA=OB=1,P是函数y=$\frac{1}{2x}$(x>0)图象上的一动点,过P作PM⊥x轴,PN⊥y轴,M、N分别为垂足,线段PM,PN分别交线段AB于E、F.求证:AF•BE=1.
如图,A、B分别是x、y轴上的点,且OA=OB=1,P是函数y=$\frac{1}{2x}$(x>0)图象上的一动点,过P作PM⊥x轴,PN⊥y轴,M、N分别为垂足,线段PM,PN分别交线段AB于E、F.求证:AF•BE=1.
分析 首先求得直线AB的解析式,然后设P的横坐标是m,则P的坐标是(m,$\frac{1}{2m}$),求得AF和BE的长,即可证明.
解答 证明:∵OA=OB=1,
∴A和B的坐标分别是(1,0)和(0,1).
设AB的解析式是y=kx+b,则$\left\{\begin{array}{l}{k+b=0}\\{b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=1}\end{array}\right.$,
则直线AB的解析式是y=-x+1.
设P的横坐标是m,则P的坐标是(m,$\frac{1}{2m}$).
在y=-x+1中,令x=m,则y=-m+1,则E的坐标是(m,-m+1).
在y=-x+1中,令y=$\frac{1}{2m}$,则$\frac{1}{2m}$=-x+1,解得x=1-$\frac{1}{2m}$,则F的坐标是(1-$\frac{1}{2m}$,$\frac{1}{2m}$).
则BE=$\sqrt{{m}^{2}+【1-(-m+1){】}^{2}}$=$\sqrt{2}$m,
AF=$\sqrt{【1-(1-\frac{1}{2m}){】}^{2}+(\frac{1}{2m})^{2}}$=$\frac{\sqrt{2}}{2m}$.
则AF•BE=$\frac{\sqrt{2}}{2m}$•$\sqrt{2}$m=1.
点评 本题考查了反比例函数的性质的综合应用,正确求得E和F的坐标,表示出AF和BE的长是本题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
8.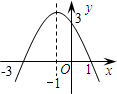 二次函数y=-x2-2x+3的图象如图所示,当y<0时,自变量x的取值范围是( )
二次函数y=-x2-2x+3的图象如图所示,当y<0时,自变量x的取值范围是( )
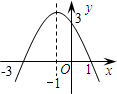 二次函数y=-x2-2x+3的图象如图所示,当y<0时,自变量x的取值范围是( )
二次函数y=-x2-2x+3的图象如图所示,当y<0时,自变量x的取值范围是( )| A. | -3<x<1 | B. | x<-3 | C. | x>1 | D. | x<-3或x>1 |

 如图所示,有一个二级台阶,每一级的长、宽、高分别为60cm,45cm,27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物,若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?
如图所示,有一个二级台阶,每一级的长、宽、高分别为60cm,45cm,27cm,A和B是这两个台阶的相对端点,A点上有一只蚂蚁想到B点去吃可口的食物,若蚂蚁平均每秒走0.8cm,则蚂蚁沿着台阶从A到B至少需要多少时间?