题目内容
5．
如图所示，有一个二级台阶，每一级的长、宽、高分别为60cm，45cm，27cm，A和B是这两个台阶的相对端点，A点上有一只蚂蚁想到B点去吃可口的食物，若蚂蚁平均每秒走0.8cm，则蚂蚁沿着台阶从A到B至少需要多少时间？
分析 根据题意画出台阶的侧面展开图，根据勾股定理求出AB的长，再由蚂蚁平均每秒走0.8cm即可得出结论．
解答 解：如图所示，
AB=$\sqrt{{60}^{2}+（45+27+45+27）^{2}}$=12$\sqrt{17}$（cm）．
∵蚂蚁平均每秒走0.8cm，
∴$\frac{12\sqrt{17}}{0.8}$=15$\sqrt{17}$（秒）．
答：蚂蚁沿着台阶从A到B至少需要15$\sqrt{17}$秒．
点评 本题考查的是平面展开-最短路径问题，根据题意画出圆柱的侧面展开图，利用勾股定理求解是解答此题的关键．
练习册系列答案
相关题目
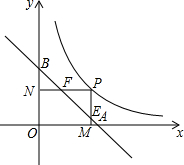如图，A、B分别是x、y轴上的点，且OA=OB=1，P是函数y=$\frac{1}{2x}$（x＞0）图象上的一动点，过P作PM⊥x轴，PN⊥y轴，M、N分别为垂足，线段PM，PN分别交线段AB于E、F．求证：AF•BE=1．
如图，在△ABC中，AD，AE，AF分别为△ABC的高线、角平分线和中线．
如图所示，在△ABC中，AD是角平分线，DE∥AC交AB于E，EF∥AD交BC于F，试问：EF是△BDE的角平分线吗？说说你的理由．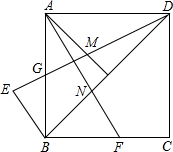
如图，在正方形ABCD中，G为AB边的中点，∠BAD的平分线交DG于M，过点B作BE⊥BD交DG的延长线于点E，再过点A作AF⊥DG，交BC边于点F，交BD边于点N．
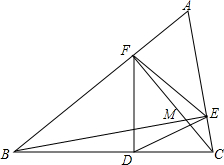如图，△ABC，∠A=60°，BE⊥AC于点F，点D是BC中点，BE与CF相交于M