题目内容
17.(1)已知:x+y=$\frac{1}{2}$,xy=1,求x3y+2x2y2+xy3的值.(2)若a-b=2,a-c=$\frac{1}{2}$,求(b-c)2+3(b-c)+$\frac{9}{4}$的值.
分析 (1)利用提公因式法和完全平方公式把代数式变形为x+y和xy的形式,再进一步整体代入求解;
(2)由a-b=2,a-c=$\frac{1}{2}$得出b-c=-$\frac{3}{2}$,进一步代入求得答案即可.
解答 解:(1)∵x+y=$\frac{1}{2}$,xy=1,
∴x3y+2x2y2+xy3
=xy(x2+2xy+y2)
=xy(x+y)2
=$\frac{1}{4}$;
(2)∵a-b=2,a-c=$\frac{1}{2}$
∴b-c=-$\frac{3}{2}$,
∴(b-c)2+3(b-c)+$\frac{9}{4}$
=$\frac{9}{4}$+3×(-$\frac{3}{2}$)+$\frac{9}{4}$
=0.
点评 此题考查了因式分解的运用,渗透整体代入的思想.

练习册系列答案
相关题目
2.下列各式的值相等的是( )
| A. | -32与-23 | B. | 32与|-2|3 | C. | -32与-(-3)2 | D. | (-3)2与-32 |
 如图,在平面直角坐标系中,已知B(8,0),C(0.6),P(-3,3),现将一直角三角板EPF的直角顶点放在点P处,EP交y轴于N,FP交x轴于M,把△EPF绕点P旋转,请问0M+ON是否为一定值?若是,求出其值;若不是,请说明理由.
如图,在平面直角坐标系中,已知B(8,0),C(0.6),P(-3,3),现将一直角三角板EPF的直角顶点放在点P处,EP交y轴于N,FP交x轴于M,把△EPF绕点P旋转,请问0M+ON是否为一定值?若是,求出其值;若不是,请说明理由.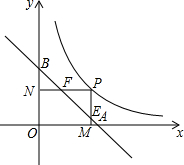 如图,A、B分别是x、y轴上的点,且OA=OB=1,P是函数y=$\frac{1}{2x}$(x>0)图象上的一动点,过P作PM⊥x轴,PN⊥y轴,M、N分别为垂足,线段PM,PN分别交线段AB于E、F.求证:AF•BE=1.
如图,A、B分别是x、y轴上的点,且OA=OB=1,P是函数y=$\frac{1}{2x}$(x>0)图象上的一动点,过P作PM⊥x轴,PN⊥y轴,M、N分别为垂足,线段PM,PN分别交线段AB于E、F.求证:AF•BE=1. 如图,在△ABC中,AD,AE,AF分别为△ABC的高线、角平分线和中线.
如图,在△ABC中,AD,AE,AF分别为△ABC的高线、角平分线和中线.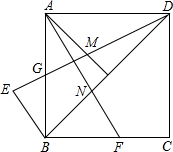 如图,在正方形ABCD中,G为AB边的中点,∠BAD的平分线交DG于M,过点B作BE⊥BD交DG的延长线于点E,再过点A作AF⊥DG,交BC边于点F,交BD边于点N.
如图,在正方形ABCD中,G为AB边的中点,∠BAD的平分线交DG于M,过点B作BE⊥BD交DG的延长线于点E,再过点A作AF⊥DG,交BC边于点F,交BD边于点N.