题目内容
1.菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为菱形或矩形的“接近度”.
(1)设菱形相邻两个内角的度数分别为m°、n°,若我们将菱形的“接近度”定义为|m-n|,于是|m-n|越小,菱形就接近正方形.
①菱形的一个内角为70°,则“接近度”=40;
②菱形的“接近度”=0时,菱形就是正方形.
(2)若我们将菱形的“接近度”定义为$\frac{m}{n}$(m<n),则:
①菱形的一个内角为60°,则“接近度”=$\frac{1}{2}$;
②在这种情况下,菱形的“接近度”=1时,菱形就是正方形.
分析 (1)①利用菱形的“接近度”定义为|m-n|,进而代入求出即可;
②根据当菱形的“接近度”等于0时,菱形的相邻的内角相等,进而得出答案;
(2)①利用菱形的“接近度”定义为$\frac{m}{n}$,进而代入求出即可;
②根据当菱形的“接近度”等于1时,菱形的相邻的内角相等,进而得出答案
解答 解:(1)①若菱形的一个内角为70°,
∴该菱形的相邻的另一内角的度数110°,
∴“接近度”等于|110-70|=40;
②当菱形的“接近度”等于0时,菱形的相邻的内角相等,因而都是90度,
则菱形是正方形;
(2)①若菱形的一个内角为60°,
∴该菱形的相邻的另一内角的度数120°,
∴“接近度”等于$\frac{60}{120}$=$\frac{1}{2}$;
②当菱形的“接近度”等于1时,菱形的相邻的内角相等,因而都是90度,
则菱形是正方形;
故答案为:40;0;$\frac{1}{2}$;1.
点评 此题主要考查了菱形的性质以及新定义,利用“接近度”定义求出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列各式的值相等的是( )
| A. | -32与-23 | B. | 32与|-2|3 | C. | -32与-(-3)2 | D. | (-3)2与-32 |
 如图,在平面直角坐标系中,已知B(8,0),C(0.6),P(-3,3),现将一直角三角板EPF的直角顶点放在点P处,EP交y轴于N,FP交x轴于M,把△EPF绕点P旋转,请问0M+ON是否为一定值?若是,求出其值;若不是,请说明理由.
如图,在平面直角坐标系中,已知B(8,0),C(0.6),P(-3,3),现将一直角三角板EPF的直角顶点放在点P处,EP交y轴于N,FP交x轴于M,把△EPF绕点P旋转,请问0M+ON是否为一定值?若是,求出其值;若不是,请说明理由.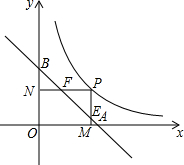 如图,A、B分别是x、y轴上的点,且OA=OB=1,P是函数y=$\frac{1}{2x}$(x>0)图象上的一动点,过P作PM⊥x轴,PN⊥y轴,M、N分别为垂足,线段PM,PN分别交线段AB于E、F.求证:AF•BE=1.
如图,A、B分别是x、y轴上的点,且OA=OB=1,P是函数y=$\frac{1}{2x}$(x>0)图象上的一动点,过P作PM⊥x轴,PN⊥y轴,M、N分别为垂足,线段PM,PN分别交线段AB于E、F.求证:AF•BE=1.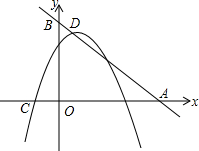 如图,直线y=-x+5与x、y轴分别交于点A、B,抛物线y=-x2+bx+c的顶点在直线AB上,且经过另一点(2,3)
如图,直线y=-x+5与x、y轴分别交于点A、B,抛物线y=-x2+bx+c的顶点在直线AB上,且经过另一点(2,3) 如图,在△ABC中,AD,AE,AF分别为△ABC的高线、角平分线和中线.
如图,在△ABC中,AD,AE,AF分别为△ABC的高线、角平分线和中线. 如图所示,在△ABC中,AD是角平分线,DE∥AC交AB于E,EF∥AD交BC于F,试问:EF是△BDE的角平分线吗?说说你的理由.
如图所示,在△ABC中,AD是角平分线,DE∥AC交AB于E,EF∥AD交BC于F,试问:EF是△BDE的角平分线吗?说说你的理由.