题目内容
4.若函数y=a(x+m)2图象是由函数y=5x2的图象向左平移$\frac{3}{2}$个单位长度得到的,则a=5,m=$\frac{3}{2}$.分析 由于抛物线平移后的形状不变,故a不变.直接根据“上加下减,左加右减”的平移规律得到抛物线y=5x2平移后的解析式.
解答 解:函数y=5x2的图象向左平移$\frac{3}{2}$个单位后的解析式为:y=5(x+$\frac{3}{2}$)2,
∵函数y=a(x+m)2图象是由函数y=5x2的图象向左平移$\frac{3}{2}$个单位长度得到的,
∴a=5,m=$\frac{3}{2}$.
故答案是:5;$\frac{3}{2}$.
点评 本题考查了二次函数图象与几何变换.由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.$\frac{a}{{m}^{2}{-n}^{2}}•(n-m)$的值为( )
| A. | $\frac{a}{m-n}$ | B. | $\frac{a}{m+n}$ | C. | -$\frac{a}{m+n}$ | D. | -$\frac{a}{m-n}$ |
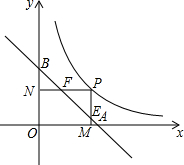 如图,A、B分别是x、y轴上的点,且OA=OB=1,P是函数y=$\frac{1}{2x}$(x>0)图象上的一动点,过P作PM⊥x轴,PN⊥y轴,M、N分别为垂足,线段PM,PN分别交线段AB于E、F.求证:AF•BE=1.
如图,A、B分别是x、y轴上的点,且OA=OB=1,P是函数y=$\frac{1}{2x}$(x>0)图象上的一动点,过P作PM⊥x轴,PN⊥y轴,M、N分别为垂足,线段PM,PN分别交线段AB于E、F.求证:AF•BE=1.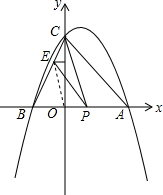 如图,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1、x2是方程x2-2x-8=0的两个根.
如图,抛物线与x轴交于A(x1,0),B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1、x2是方程x2-2x-8=0的两个根.