题目内容
13．
在平行四边形ABCD中，点E是边AB的中点，AC、DE交于点F，则AF：FC=1：2．
分析 先证明△AFE∽△CFD，然后利用相似三角形的性质即可求出答案．
解答 解：∵AE∥CD，
∴△AFE∽△CFD，
$\frac{AF}{CF}=\frac{AE}{CD}$，
∵点E是AB的中点，
∴$\frac{AE}{CD}$=$\frac{1}{2}$，
∴$\frac{AF}{FC}$=$\frac{1}{2}$
故答案为：1：2
点评 本题考查相似三角形的性质与判定，解题的关键是熟练运用相似三角形的判定，本题属于基础题型．
练习册系列答案
相关题目
如图，已知点O为平行四边形ABCD所在平面上一点，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，求$\overrightarrow{OD}$（用$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$表示）
4．有9名同学参加歌咏比赛，他们的预赛成绩各不相同，现取其中前4名参加决赛，小红同学在知道自己成绩的情况下，要判断自己能否进入决赛，还需要知道这9名同学成绩的（ ）
| A． | 平均数 | B． | 方差 | C． | 中位数 | D． | 极差 |
1．
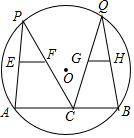如图，P、Q两点是半径为2cm的⊙O上的两动点，E、F分别是弦PA、PC的中点，G、H分别是弦QC、QB的中点，则EF+GH的值（ ）
如图，P、Q两点是半径为2cm的⊙O上的两动点，E、F分别是弦PA、PC的中点，G、H分别是弦QC、QB的中点，则EF+GH的值（ ）| A． | 随着P、Q的运动而变化 | |
| B． | 等于2cm | |
| C． | P、Q两点在弦AB同侧时，EF+GH为定值，在AB异侧时不为定值 | |
| D． | 等于AB的一半 |
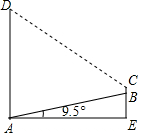如图，AB为一斜坡，其坡角为19.5°，紧挨着斜坡AB底部A处有一高楼，一数学活动小组量得斜坡长AB=15m，在坡顶B处测得楼顶D处的仰角为45°，其中测量员小刚的身高BC=1.7米，求楼高AD．
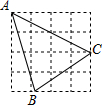如图，在4×4的方格纸中有一格点△ABC，若△ABC的面积为$\frac{21}{2}$cm2，则这张方格纸的面积等于24cm2．