题目内容
18.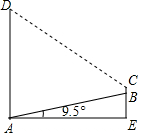 如图,AB为一斜坡,其坡角为19.5°,紧挨着斜坡AB底部A处有一高楼,一数学活动小组量得斜坡长AB=15m,在坡顶B处测得楼顶D处的仰角为45°,其中测量员小刚的身高BC=1.7米,求楼高AD.
如图,AB为一斜坡,其坡角为19.5°,紧挨着斜坡AB底部A处有一高楼,一数学活动小组量得斜坡长AB=15m,在坡顶B处测得楼顶D处的仰角为45°,其中测量员小刚的身高BC=1.7米,求楼高AD.(参考数据:sin19.5°≈$\frac{1}{3}$,tan19.5°≈$\frac{7}{20}$,最终结果精确到0.1m).
分析 作CF⊥AD于点F,在直角△ABE中求得BE,和AE的长,然后在直角△CDE中利用三角函数求得DE的长,根据AD=DF+AF=CF+BC+BE求解.
解答 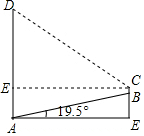 解:作CF⊥AD于点F.
解:作CF⊥AD于点F.
在Rt△ABE中,∵AB=15,
∴BE=ABsin19.5°=15sin19.5°,
AE=ABcos19.5°=15cos19.5°,
在Rt△CDF中,∵CF=AE,∠DCF=45°,
∴DF=CF,
∴AD=DF+AF=CF+BC+BE=15cos19.5°+1.7+15sin19.5°≈21.0(m).
答:楼高AD为21.0米.
点评 本题考查了解直角三角形的应用-仰角俯角问题,还考查的知识点有三角函数、直角三角形的性质以及勾股定理等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.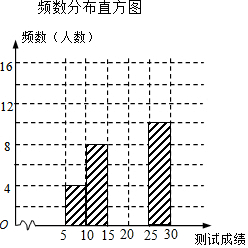 某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:
某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:
频数分布表
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于15分为合格,请你估计该校七年级学生有理数混合运算能力测试合格的人数?
 某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:
某校为了调查初一年级学生有理数混合运算能力,从七年级400名学生中堆积抽选50名学生参加测试,对这50名学生同时进行30个有理数混合运算的考察,每做正确1个得1分,根据测试成绩绘制出不完整的频数分布直方图如下图表:频数分布表
| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 5≤x<10 | 4 |
| 第2组 | 10≤x<15 | 8 |
| 第3组 | 15≤x<20 | 16 |
| 第4组 | 20≤x<25 | a |
| 第5组 | 25≤x<30 | b |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于15分为合格,请你估计该校七年级学生有理数混合运算能力测试合格的人数?




 在平行四边形ABCD中,点E是边AB的中点,AC、DE交于点F,则AF:FC=1:2.
在平行四边形ABCD中,点E是边AB的中点,AC、DE交于点F,则AF:FC=1:2. 一个几何体由几个相同的小正方体搭成,它的三视图如图所示,搭成这个几何体的小正方体的个数是( )
一个几何体由几个相同的小正方体搭成,它的三视图如图所示,搭成这个几何体的小正方体的个数是( )
 如图,在边长为1的小正反形组成的网格中,△ABC的三个顶点均在格点上,则tanB的值为$\frac{3}{4}$.
如图,在边长为1的小正反形组成的网格中,△ABC的三个顶点均在格点上,则tanB的值为$\frac{3}{4}$.