题目内容
17. 如图,直线y=mx+n与双曲线y=$\frac{k}{x}$相交于A(-1,2)、B(2,b)两点,与y轴相交于点C.
如图,直线y=mx+n与双曲线y=$\frac{k}{x}$相交于A(-1,2)、B(2,b)两点,与y轴相交于点C.(1)求m,n的值;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)在坐标轴上是否存在异于D点的点P,使得S△PAB=S△DAB?若存在,直接写出P点坐标;若不存在,说明理由.
分析 (1)利用待定系数法求出m,n的值;
(2)根据关于x轴对称的点的坐标特征求出点D的坐标,利用三角形面积公式计算即可;
(3)分点P在x轴上和点P在y轴上两种情况,利用三角形面积公式计算即可.
解答 解:(1)∵点A(-1,2)在双曲线y=$\frac{k}{x}$上,
∴2=$\frac{k}{-1}$,
解得,k=-2,
∴反比例函数解析式为:y=-$\frac{2}{x}$,
∴b=$\frac{-2}{2}$=-1,
则点B的坐标为(2,-1),
∴$\left\{\begin{array}{l}{-m+n=2}\\{2m+n=-1}\end{array}\right.$,
解得,m=-1,n=1;
(2)对于y=-x+1,当x=0时,y=1,
∴点C的坐标为(0,1),
∵点D与点C关于x轴对称,
∴点D的坐标为(0,-1),
∴△ABD的面积=$\frac{1}{2}$×2×3=3;
(3)对于y=-x+1,当y=0时,x=1,
∴直线y=-x+1与x轴的交点坐标为(0,1),
当点P在x轴上时,设点P的坐标为(a,0),
S△PAB=$\frac{1}{2}$×|1-a|×2+$\frac{1}{2}$×|1-a|×1=3,
解得,a=-1或3,
当点P在y轴上时,设点P的坐标为(0,b),
S△PAB=$\frac{1}{2}$×|1-b|×2+$\frac{1}{2}$×|1-b|×1=3,
解得,b=-1或3,
∴P点坐标为(-1,0)或(3,0)或(0,-1)或(0,3).
点评 本题考查的是反比例函数与一次函数的交点问题,掌握待定系数法求函数解析式的一般步骤、函数图象上点的坐标特征是解题的关键.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
7.袋中装有除颜色外完全相同的a个白球、b个红球、c个黄球,则任意摸出一个球是黄球的概率为( )
| A. | $\frac{c}{a+b+c}$ | B. | $\frac{c}{a+b}$ | C. | $\frac{a+c}{a+b+c}$ | D. | $\frac{a+b}{c}$ |
12.已知方程x-2=2x+1的解与方程k(x-2)=$\frac{x+1}{2}$的解相同,则k的值是( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | 2 | D. | -2 |
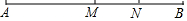 如图所示,点M,N是线段AB上的两个点,且M是AB的中点,N是MB的中点,若AB=a,NB=b,下列结论:①AM=$\frac{1}{2}$a②AN=a-b③MN=$\frac{1}{2}$a-b④MN=$\frac{1}{4}$a.其中正确的有( )
如图所示,点M,N是线段AB上的两个点,且M是AB的中点,N是MB的中点,若AB=a,NB=b,下列结论:①AM=$\frac{1}{2}$a②AN=a-b③MN=$\frac{1}{2}$a-b④MN=$\frac{1}{4}$a.其中正确的有( )
 如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.