Question

7．如图是一个长为2a、宽为2b的长方形，沿图中虚线用剪刀均匀分成四块小长方形，然后按图2形状拼成一个正方形．
（1）请利用图2中的空白部分面积的不同表示方法，写出一个关于a、b的恒等式（a+b）²=（a-b）²+4ab．
（2）若a+b=10，ab=6，根据你所得到的恒等式，求（a-b）的值．

Answer 1

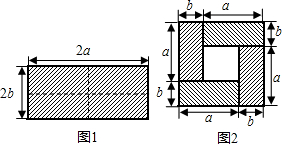
分析 （1）阴影部分的面积可以看作是边长（a-b）的正方形的面积，也可以看作边长（a+b）的正方形的面积减去4个小长方形的面积；
（2）利用（1）的结论，把（a-b）²=（a+b）²-4ab，把数值整体代入即可．

解答 解：（1）恒等式为：（a+b）²=（a-b）²+4ab．
例如：当a=5，b=2时，
（a+b）²=（5+2）²=49
（a-b）²=（5-2）²=9
4ab=4×5×2=40
因为49=40+9，
所以（a+b）²=（a-b）²+4ab．
故答案为：：（a+b）²=（a-b）²+4ab．
（2）∵a+b=10，
（a+b）²=100，
∵（a+b）²=（a-b）²+4ab，ab=6，
∴（a-b）²=（a+b）²-4ab=100-4×6=76，
∴a-b=2$\sqrt{19}$或a-b=-2$\sqrt{19}$，
∵a＞b，
∴a-b=2$\sqrt{19}$．

点评 本题考查了列代数式，完全平方公式的实际应用，完全平方公式与正方形的面积公式和长方形的面积公式经常联系在一起．要学会观察．