题目内容
16.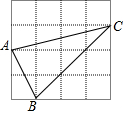 如图,在4×4的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则该三角形最长边的长为( )
如图,在4×4的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则该三角形最长边的长为( )| A. | $\sqrt{5}$ | B. | $\sqrt{17}$ | C. | $3\sqrt{2}$ | D. | $5\sqrt{2}$ |
分析 根据勾股定理求出各边长,比较即可.
解答 解:由勾股定理得,AC=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$,
AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
BC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∵$\sqrt{5}$<$\sqrt{17}$<3$\sqrt{2}$,
∴该三角形最长边的长为3$\sqrt{2}$,
故选:C.
点评 本题考查的是勾股定理的应用,直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
相关题目
6.下列图形属于平移位置变换的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,AD=CB,AB=CD,求证:△ACB≌△CAD.
如图,AD=CB,AB=CD,求证:△ACB≌△CAD.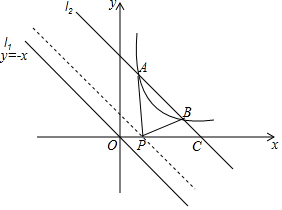 如图,已知一次函数y=-x的图象是直线l1,将它向上平移4个单位得到了直线l2,直线l2与反比例函数的图象交于A(1,m)和B(n,1),与x轴交于点C.
如图,已知一次函数y=-x的图象是直线l1,将它向上平移4个单位得到了直线l2,直线l2与反比例函数的图象交于A(1,m)和B(n,1),与x轴交于点C.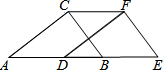 如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.
如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.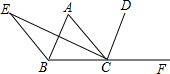 如图所示,已知BA平分∠EBC,CD平分∠ACF,且AB∥CD,
如图所示,已知BA平分∠EBC,CD平分∠ACF,且AB∥CD, 如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为点E.连接DE,则线段DE与线段AC有怎样的数量关系?请证明你的结论.
如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为点E.连接DE,则线段DE与线段AC有怎样的数量关系?请证明你的结论.