题目内容
4.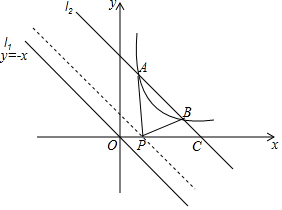 如图,已知一次函数y=-x的图象是直线l1,将它向上平移4个单位得到了直线l2,直线l2与反比例函数的图象交于A(1,m)和B(n,1),与x轴交于点C.
如图,已知一次函数y=-x的图象是直线l1,将它向上平移4个单位得到了直线l2,直线l2与反比例函数的图象交于A(1,m)和B(n,1),与x轴交于点C.(1)直线l2的函数关系式是y=-x+4
(2)求m、n的值及反比例函数的关系式;
(3)在直线l1平移得到直线l2的过程中,直线l1与x轴交于点P(含与点O重合),连结PA,PB.设点P的坐标为(t,0),△PAB的面积为S,请求出用t表示S的函数关系式,并说明当t为何值时,△PAB面积S最大.
分析 (1)由平移的性质可求得答案;
(2)把A、B两点的坐标代入直线l2的解析式可分别求得m、n的值,代入反比例函数解析式可求得反比例函数解析式;
(3)用t可表示出PC的长,结合A、B的坐标可分别表示出△PAC和△PBC的面积,利用S=S△PAC-S△PBC可求得S与t的函数关系式,利用函数的性质可求得S的最大值.
解答 解:
(1)∵直线l1的解析式为y=-x,
∴将它向上平移4个单位其解析式为y=-x+4,
∴直线l2的函数关系式是y=-x+4,
故答案为:y=-x+4;
(2)∵直线l2与反比例函数的图象交于A(1,m)和B(n,1),
∴m=-1+4=3,1=-n+4,
∴m=3,n=3,
∴A(1,3),B(3,1),
设反比例函数解析式为y=$\frac{k}{x}$,
∴k=1×3=3,
∴反比例函数解析式为y=$\frac{3}{x}$;
(3)在y=-x+4中,令y=0可求得x=4,
∴C(4,0),
∵P(t,0)(0≤t≤4),
∴PC=4-t,
∴S=S△PAC-S△PBC=$\frac{1}{2}$PC×3-$\frac{1}{2}$PC×1=PC=4-t,
即S=-t+4,
∴S随t的增大而减小,
∴当t=0时,S有最大值4.
点评 本题为反比例函数的综合应用,涉及平移的性质、待定系数法、函数图象上点的坐标特征、三角形面积及一次函数的性质等知识.在(1)中掌握平移的性质是解题的关键,在(2)中求得A、B的坐标是解题的关键,在(3)中用t表示出△PAB的面积是解题的关键.本题考查知识点较多,综合性较强,难度适中.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
14.下列式子成立的是( )
| A. | 3a+4a=7a | B. | -7x2+5x2=-2 | C. | 2a2b-2b2a=0 | D. | 3a+4b=7ab |
16.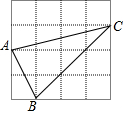 如图,在4×4的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则该三角形最长边的长为( )
如图,在4×4的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则该三角形最长边的长为( )
 如图,在4×4的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则该三角形最长边的长为( )
如图,在4×4的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则该三角形最长边的长为( )| A. | $\sqrt{5}$ | B. | $\sqrt{17}$ | C. | $3\sqrt{2}$ | D. | $5\sqrt{2}$ |
13.已知x>y,下列不等式一定成立的是( )
| A. | x-8<y-8 | B. | 5x<5y | C. | -7x<-7y | D. | 3y+1>3x+1 |
14. 把一块直角三角板的直角顶点放在直尺的一边上,如图所示,现用量角器量得∠2=112°,则∠1的度数为( )
把一块直角三角板的直角顶点放在直尺的一边上,如图所示,现用量角器量得∠2=112°,则∠1的度数为( )
 把一块直角三角板的直角顶点放在直尺的一边上,如图所示,现用量角器量得∠2=112°,则∠1的度数为( )
把一块直角三角板的直角顶点放在直尺的一边上,如图所示,现用量角器量得∠2=112°,则∠1的度数为( )| A. | 30° | B. | 28° | C. | 22° | D. | 20° |
 如图所示,已知 FC∥AB∥DE,∠α:∠D:∠B=2:3:4,则∠B=144度.
如图所示,已知 FC∥AB∥DE,∠α:∠D:∠B=2:3:4,则∠B=144度.