题目内容
8. 如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为点E.连接DE,则线段DE与线段AC有怎样的数量关系?请证明你的结论.
如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为点E.连接DE,则线段DE与线段AC有怎样的数量关系?请证明你的结论.
分析 由等腰三角形的性质和平行线的性质得出可得∠ADC=90°,∠ADC=90°,得出四边形ADCE为矩形,即可得出结论.
解答 解:AC=DE,理由如下:
∵CE⊥AE,
∴∠AEC=90°
∵AE∥BC,
∴∠DCE=90°,
∵AB=AC AD是BC边上的中线,
∴∠ADC=90°,
∴四边形ADCE是矩形,
∴AC=DE.
点评 此题考查了矩形的判定与性质、等腰三角形的性质、平行线的性质.熟练掌握等腰三角形的性质,证明四边形ADCE是矩形是解决问题的关键.

练习册系列答案
相关题目
18.下列事件中,是确定事件的是( )
| A. | 打开电视机,它正在播放广告 | |
| B. | 明天一定是天晴 | |
| C. | 任意掷一枚质地均匀的骰子,掷出的点数是奇数 | |
| D. | 抛出的篮球会下落 |
16.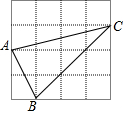 如图,在4×4的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则该三角形最长边的长为( )
如图,在4×4的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则该三角形最长边的长为( )
 如图,在4×4的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则该三角形最长边的长为( )
如图,在4×4的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则该三角形最长边的长为( )| A. | $\sqrt{5}$ | B. | $\sqrt{17}$ | C. | $3\sqrt{2}$ | D. | $5\sqrt{2}$ |
3.在△ABC中,D、E分别是AB边和AC边的中点,若DE的长是2,则BC的长为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.已知x>y,下列不等式一定成立的是( )
| A. | x-8<y-8 | B. | 5x<5y | C. | -7x<-7y | D. | 3y+1>3x+1 |
 如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.