题目内容
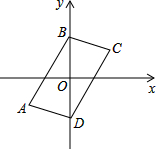如图，在平面直角坐标系中，四边形ABCD的四个顶点坐标分别为A（-3，-2），B（0，3），C（3，2），D（0，-3）．四边形ABCD是不是平行四边形？请给出证明．考点：平行四边形的判定,坐标与图形性质
专题：
分析：直接根据A，B，C，D点的坐标，进而得出AB，CD，BC，AD的长，进而利用平行四边形的判定得出即可．
解答：解：四边形ABCD是平行四边形．
理由：∵A（-3，-2），B（0，3），C（3，2），D（0，-3），
∴AB=
=
，
CD=
=
，
BC=
=
，
AD=
=
，
∴AB=CD，BC=AD，
∴四边形ABCD是平行四边形．
理由：∵A（-3，-2），B（0，3），C（3，2），D（0，-3），
∴AB=
| 52+32 |
| 34 |
CD=
| 52+32 |
| 34 |
BC=
| 12+32 |
| 10 |
AD=
| 12+32 |
| 10 |
∴AB=CD，BC=AD，
∴四边形ABCD是平行四边形．
点评：此题主要考查了平行四边形的判定以及点的坐标性质，得出各边长是解题关键．
练习册系列答案
相关题目
给定下列条件，不能判定三角形是直角三角形的是（ ）
| A、∠A+∠B=∠C |
| B、∠A：∠B：∠C=1：2：3 |
| C、2∠A=3∠B=4∠C |
| D、∠A一∠B=∠C |
四边形的四边依次为a，b，c，d，且满足a2+b2+c2+d2-ab-bc-ad-cd=0，则四边形是（ ）
| A、平行四边形 | B、矩形 |
| C、菱形 | D、正方形 |
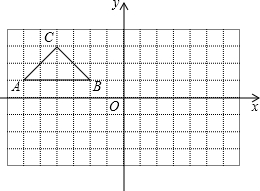如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：
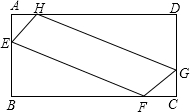为了美化校园环境，某校准备在一块空地（如图所示的长方形ABCD，AB=10m，BC=20m）上进行绿化，中间的一块（图中四边形EFGH）上种花，其他的四块（图中的四个直角三角形）上铺设草坪，并要求AE=AH=CF=CG，那么在满足上述条件的所有设计中，是否存在一种设计，使得四边形EFGH的面积最大？
如图，已知O为坐标原点，将直线y=x向右平移2个单位后与双曲线y=