题目内容
电压一定时,电阻R与电流强度I成反比例,且当R=10Ω时,I=0.3A.求:
(1)I关于R的函数解析式,并指出它是什么函数;
(2)当R=4Ω时的电流强度;
(3)当I=0.5A时的电阻.
(1)I关于R的函数解析式,并指出它是什么函数;
(2)当R=4Ω时的电流强度;
(3)当I=0.5A时的电阻.
考点:反比例函数的应用
专题:
分析:(1)根据电阻R与电流强度I成反比例利用待定系数法确定反比例函数的解析式,然后说明其是什么函数即可;
(2)代入R=4Ω即可求得电流强度;
(3)代入I=0.5A即可求得电阻.
(2)代入R=4Ω即可求得电流强度;
(3)代入I=0.5A即可求得电阻.
解答:解:(1)∵电阻R与电流强度I成反比例,
∴设解析式为:R=
,
∵当R=10Ω时,I=0.3A.
∴K=RI=10×0.3=3,
∴解析式为:R=
,
∴是反比例函数;
(2)当R=4Ω时,
I=
=0.75A;
(3)当I=0.5A时,
R=
=6Ω.
∴设解析式为:R=
| k |
| I |
∵当R=10Ω时,I=0.3A.
∴K=RI=10×0.3=3,
∴解析式为:R=
| 3 |
| I |
∴是反比例函数;
(2)当R=4Ω时,
I=
| 3 |
| 4 |
(3)当I=0.5A时,
R=
| 3 |
| 0.5 |
点评:本题考查了反比例函数的应用,解题的关键是了解电阻与电流之间的关系,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若正方形的边长为6,边长增加x,面积增加y,则y关于x的函数解析式为( )
| A、y=(x+6)2 |
| B、y=x2+62 |
| C、y=x2+6x |
| D、y=x2+12x |
二次函数y=-x2-8x+c的最大值为0,则c的值等于( )
| A、4 | B、-4 | C、-16 | D、16 |
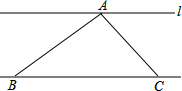 如图,△ABC的面积是2cm2,直线l∥BC,顶点A在l上,当顶点C沿BC所在直线向点B运动(不超过点B)时,要保持△ABC的面积不变,则顶点A应( )
如图,△ABC的面积是2cm2,直线l∥BC,顶点A在l上,当顶点C沿BC所在直线向点B运动(不超过点B)时,要保持△ABC的面积不变,则顶点A应( )| A、向直线l的上方运动 |
| B、向直线l的下方运动 |
| C、在直线l上运动 |
| D、以上三种情形都可能发生 |
 用小立方体搭成的几何体的主视图和左视图如图所示,则搭成这个几何体至少要多少个小立方体?最多要多少个小立方体?
用小立方体搭成的几何体的主视图和左视图如图所示,则搭成这个几何体至少要多少个小立方体?最多要多少个小立方体? 已知:如图,AB=AC,AD∥BC,O是∠ABC和∠ACB平分线的交点,CO的延长线交AD于D.求证:DB⊥OB.
已知:如图,AB=AC,AD∥BC,O是∠ABC和∠ACB平分线的交点,CO的延长线交AD于D.求证:DB⊥OB.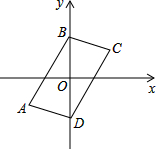 如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(-3,-2),B(0,3),C(3,2),D(0,-3).四边形ABCD是不是平行四边形?请给出证明.
如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(-3,-2),B(0,3),C(3,2),D(0,-3).四边形ABCD是不是平行四边形?请给出证明. 如图,已知直角扇形AOB的半径OA=2cm,以OB为直径在扇形内作半圆M,过点M引MP∥AO交
如图,已知直角扇形AOB的半径OA=2cm,以OB为直径在扇形内作半圆M,过点M引MP∥AO交