题目内容
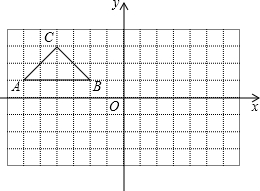 如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(1)作出格点△ABC关于原点O对称的△A1B1C1;
(2)写出点A1,B1,C1的坐标,并求出△A1B1C1的周长.
考点:作图-旋转变换
专题:作图题
分析:(1)根据网格结构找出点A、B、C关于原点O的对称点A1、B1、C1的位置,然后顺次连接即可;
(2)根据平面直角坐标系写出各点的坐标,再根据勾股定理列式求出A1C1=B1C1,然后根据三角形的周长的定义列式计算即可得解.
(2)根据平面直角坐标系写出各点的坐标,再根据勾股定理列式求出A1C1=B1C1,然后根据三角形的周长的定义列式计算即可得解.
解答: 解:(1)△A1B1C1如图所示;
解:(1)△A1B1C1如图所示;
(2)A1(6,-1),B1(2,-1),C1(4,-2),
由勾股定理得,A1C1=B1C1=
=2
,
又A1B1=6-2=4,
∴△A1B1C1的周长=2×2
+4=4
+4.
 解:(1)△A1B1C1如图所示;
解:(1)△A1B1C1如图所示;(2)A1(6,-1),B1(2,-1),C1(4,-2),
由勾股定理得,A1C1=B1C1=
| 22+22 |
| 2 |
又A1B1=6-2=4,
∴△A1B1C1的周长=2×2
| 2 |
| 2 |
点评:本题考查了利用旋转变换作图,勾股定理的应用,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 如图,△ABC和△DEF是位似图形,且D是OA的中点,则
如图,△ABC和△DEF是位似图形,且D是OA的中点,则| EF |
| BC |
A、
| ||
B、
| ||
C、
| ||
D、
|
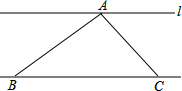 如图,△ABC的面积是2cm2,直线l∥BC,顶点A在l上,当顶点C沿BC所在直线向点B运动(不超过点B)时,要保持△ABC的面积不变,则顶点A应( )
如图,△ABC的面积是2cm2,直线l∥BC,顶点A在l上,当顶点C沿BC所在直线向点B运动(不超过点B)时,要保持△ABC的面积不变,则顶点A应( )| A、向直线l的上方运动 |
| B、向直线l的下方运动 |
| C、在直线l上运动 |
| D、以上三种情形都可能发生 |
 已知:如图,AB=AC,AD∥BC,O是∠ABC和∠ACB平分线的交点,CO的延长线交AD于D.求证:DB⊥OB.
已知:如图,AB=AC,AD∥BC,O是∠ABC和∠ACB平分线的交点,CO的延长线交AD于D.求证:DB⊥OB.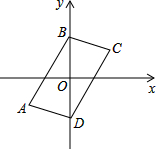 如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(-3,-2),B(0,3),C(3,2),D(0,-3).四边形ABCD是不是平行四边形?请给出证明.
如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(-3,-2),B(0,3),C(3,2),D(0,-3).四边形ABCD是不是平行四边形?请给出证明.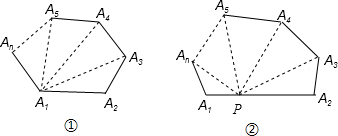
 如图,已知直角扇形AOB的半径OA=2cm,以OB为直径在扇形内作半圆M,过点M引MP∥AO交
如图,已知直角扇形AOB的半径OA=2cm,以OB为直径在扇形内作半圆M,过点M引MP∥AO交
 如图,A,B表示教室的门框位置,小聪站在教室内的点P位置,小慧、小红、小杰三位同学分别站在教室外点C,D,E的位置.这三位同学中,小聪能看见谁?看不见谁?试用盲区的意义给出解释.
如图,A,B表示教室的门框位置,小聪站在教室内的点P位置,小慧、小红、小杰三位同学分别站在教室外点C,D,E的位置.这三位同学中,小聪能看见谁?看不见谁?试用盲区的意义给出解释.