题目内容
 如图,已知O为坐标原点,将直线y=x向右平移2个单位后与双曲线y=
如图,已知O为坐标原点,将直线y=x向右平移2个单位后与双曲线y=| a |
| x |
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:直线y=x向右平移2个单位后的解析式是y=x-2,与双曲线y=
有唯一公共点,则两个解析式组成的方程组只有一个解,利用根的判别式即可求得a的值,进而求得A的坐标,x轴平分△AOB的面积,则B的纵坐标与A的纵坐标互为相反数,即可求得B的纵坐标,代入AB的解析式即可求得B的坐标,利用待定系数法即可求得k的值.
| a |
| x |
解答:解:直线y=x向右平移2个单位后的解析式是y=x-2,
根据题意得:x-2=
,则x2-2x-a=0,
△=4+4a=0,
解得:a=-1,
解方程组
,
解得:
,
则A的坐标是(1,-1),
∵x轴平分△AOB的面积,
∴B的纵坐标是1,
在y=x-2中,令y=1,解得:x=3,
则B的坐标是(3,1),
代入y=
得:k=3.
根据题意得:x-2=
| a |
| x |
△=4+4a=0,
解得:a=-1,
解方程组
|
解得:
|
则A的坐标是(1,-1),
∵x轴平分△AOB的面积,
∴B的纵坐标是1,
在y=x-2中,令y=1,解得:x=3,
则B的坐标是(3,1),
代入y=
| k |
| x |
点评:本题考查了待定系数法求函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
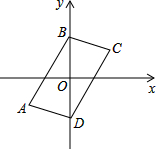 如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(-3,-2),B(0,3),C(3,2),D(0,-3).四边形ABCD是不是平行四边形?请给出证明.
如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(-3,-2),B(0,3),C(3,2),D(0,-3).四边形ABCD是不是平行四边形?请给出证明. 已知,△ABC中,AB=AC,在AB上取一点D,在AC延长线上取一点E,连接DE交BC于点F.若F是DE中点,求证:BD=CE.
已知,△ABC中,AB=AC,在AB上取一点D,在AC延长线上取一点E,连接DE交BC于点F.若F是DE中点,求证:BD=CE. 如图,A,B表示教室的门框位置,小聪站在教室内的点P位置,小慧、小红、小杰三位同学分别站在教室外点C,D,E的位置.这三位同学中,小聪能看见谁?看不见谁?试用盲区的意义给出解释.
如图,A,B表示教室的门框位置,小聪站在教室内的点P位置,小慧、小红、小杰三位同学分别站在教室外点C,D,E的位置.这三位同学中,小聪能看见谁?看不见谁?试用盲区的意义给出解释.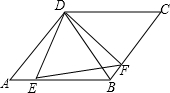 如图所示,在平行四边形ABCD中,∠A=60°,CD=BC,E,F分别在AB和BC上,且∠EDF=60°.
如图所示,在平行四边形ABCD中,∠A=60°,CD=BC,E,F分别在AB和BC上,且∠EDF=60°.