题目内容
四边形的四边依次为a,b,c,d,且满足a2+b2+c2+d2-ab-bc-ad-cd=0,则四边形是( )
| A、平行四边形 | B、矩形 |
| C、菱形 | D、正方形 |
考点:因式分解的应用
专题:
分析:通过整理配方式子a2+b2+c2+d2-ab-bc-ad-cd=0,得到(a-b)2+(b-c)2+(c-d)2+(a-d)2=0,从而得出a=b=c=d,判定四边形一定是菱形.
解答:解:∵a2+b2+c2+d2-ab-bc-ad-cd=0,
∴2(a2+b2+c2+d2-ab-bc-ad-cd)=0,
∴(a-b)2+(b-c)2+(c-d)2+(a-d)2=0,
由非负数的性质可知:(a-b)=0,(b-c)=0,(c-d)=0,(a-d)=0,
∴a=b=c=d,
∴四边形一定是菱形.
故选:C.
∴2(a2+b2+c2+d2-ab-bc-ad-cd)=0,
∴(a-b)2+(b-c)2+(c-d)2+(a-d)2=0,
由非负数的性质可知:(a-b)=0,(b-c)=0,(c-d)=0,(a-d)=0,
∴a=b=c=d,
∴四边形一定是菱形.
故选:C.
点评:此题主要考查了菱形的判定,关键是整理配方式子,还利用了非负数的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
等腰三角形的边长分别为6cm,6cm,8cm,则顶角约为( )
| A、83.62° |
| B、93.39° |
| C、67.38° |
| D、72° |
下列图案中的哪一个可以看成是由图案自身的一部分经平移后而得到的?( )
A、 |
B、 |
C、 |
D、 |
二次函数y=-x2-8x+c的最大值为0,则c的值等于( )
| A、4 | B、-4 | C、-16 | D、16 |
已知抛物线y=x2-2013x+2014与x轴的交点为(m,0),(n,0),则(m2-2013m+2014)+(n2-2013n+2014)的值是( )
| A、0 | B、2013 |
| C、2014 | D、2015 |
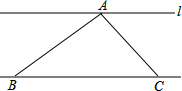 如图,△ABC的面积是2cm2,直线l∥BC,顶点A在l上,当顶点C沿BC所在直线向点B运动(不超过点B)时,要保持△ABC的面积不变,则顶点A应( )
如图,△ABC的面积是2cm2,直线l∥BC,顶点A在l上,当顶点C沿BC所在直线向点B运动(不超过点B)时,要保持△ABC的面积不变,则顶点A应( )| A、向直线l的上方运动 |
| B、向直线l的下方运动 |
| C、在直线l上运动 |
| D、以上三种情形都可能发生 |
 用小立方体搭成的几何体的主视图和左视图如图所示,则搭成这个几何体至少要多少个小立方体?最多要多少个小立方体?
用小立方体搭成的几何体的主视图和左视图如图所示,则搭成这个几何体至少要多少个小立方体?最多要多少个小立方体?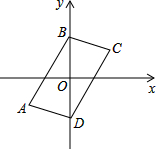 如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(-3,-2),B(0,3),C(3,2),D(0,-3).四边形ABCD是不是平行四边形?请给出证明.
如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(-3,-2),B(0,3),C(3,2),D(0,-3).四边形ABCD是不是平行四边形?请给出证明. 已知,△ABC中,AB=AC,在AB上取一点D,在AC延长线上取一点E,连接DE交BC于点F.若F是DE中点,求证:BD=CE.
已知,△ABC中,AB=AC,在AB上取一点D,在AC延长线上取一点E,连接DE交BC于点F.若F是DE中点,求证:BD=CE.