题目内容
8.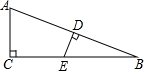 如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )
如图,Rt△ABC中,∠ACB=90°,AC=5,BC=12,AB的中垂线与BC交于点E,则BE的长等于( )| A. | $\frac{12}{5}$ | B. | $\frac{13}{5}$ | C. | $\frac{169}{24}$ | D. | $\frac{60}{13}$ |
分析 根据勾股定理求出AB的长,根据中垂线的定义和相似三角形的判定定理得到△BDE∽△BCA,根据相似三角形的性质列出比例式,计算即可.
解答 解:∵∠ACB=90°,AC=5,BC=12,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,
∵DE是AB的中垂线,
∴BD=AD=6.5,
∵DE⊥AB,∠ACB=90°,
∴△BDE∽△BCA,
∴$\frac{BD}{BC}$=$\frac{BE}{BA}$,即$\frac{6.5}{12}$=$\frac{BE}{13}$,
解得,BE=$\frac{169}{24}$,
故选:C.
点评 本题考查的是线段垂直平分线的概念和性质以及勾股定理的应用,掌握线段垂直平分线的定义、相似三角形的判定定理是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
19.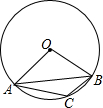 如图,△ABC为⊙O的内接三角形,∠AOB=100°,则∠ACB的度数为( )
如图,△ABC为⊙O的内接三角形,∠AOB=100°,则∠ACB的度数为( )
 如图,△ABC为⊙O的内接三角形,∠AOB=100°,则∠ACB的度数为( )
如图,△ABC为⊙O的内接三角形,∠AOB=100°,则∠ACB的度数为( )| A. | 100° | B. | 130° | C. | 150° | D. | 160° |
20.满足$-\sqrt{3}<x<\sqrt{7}$的整数共有( )个.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
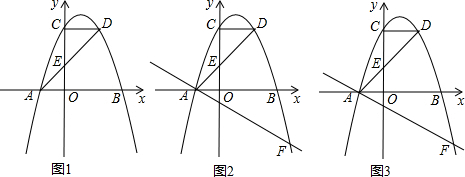
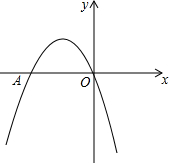 如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴交于点A(-2,0).
如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴交于点A(-2,0). 如图,⊙O的直径CD⊥AB,∠A=30°,则∠D=30°.
如图,⊙O的直径CD⊥AB,∠A=30°,则∠D=30°.