题目内容
17.三个有理数a,b,c,满足abc>0,求$\frac{a}{|\begin{array}{l}{a}\\{\;}\end{array}|}+\frac{b}{|\begin{array}{l}{b}\\{\;}\end{array}|}+\frac{c}{|\begin{array}{l}{c}\\{\;}\end{array}|}$的值.分析 根据题意,由于abc>0,依据有理数乘法法则分类讨论即可.
解答 解:由abc>0可得出:
(1)a为负,则b、c异号,负因数有2个,$\frac{a}{|\begin{array}{l}{a}\\{\;}\end{array}|}+\frac{b}{|\begin{array}{l}{b}\\{\;}\end{array}|}+\frac{c}{|\begin{array}{l}{c}\\{\;}\end{array}|}$=-1-1+1=-1;
(2)b为负,则a、c异号,负因数有2个,$\frac{a}{|\begin{array}{l}{a}\\{\;}\end{array}|}+\frac{b}{|\begin{array}{l}{b}\\{\;}\end{array}|}+\frac{c}{|\begin{array}{l}{c}\\{\;}\end{array}|}$=-1-1+1=-1;
(3)c为负,则a、b异号,负因数有2个,$\frac{a}{|\begin{array}{l}{a}\\{\;}\end{array}|}+\frac{b}{|\begin{array}{l}{b}\\{\;}\end{array}|}+\frac{c}{|\begin{array}{l}{c}\\{\;}\end{array}|}$=-1-1+1=-1;
(4)c为正,则a、b为正,负因数有0个,$\frac{a}{|\begin{array}{l}{a}\\{\;}\end{array}|}+\frac{b}{|\begin{array}{l}{b}\\{\;}\end{array}|}+\frac{c}{|\begin{array}{l}{c}\\{\;}\end{array}|}$=1+1+1=3;
所以$\frac{a}{|\begin{array}{l}{a}\\{\;}\end{array}|}+\frac{b}{|\begin{array}{l}{b}\\{\;}\end{array}|}+\frac{c}{|\begin{array}{l}{c}\\{\;}\end{array}|}$的值是-1或3.
点评 本题考查了有理数的乘法,几个不等于零的数相乘,积的符号由负因数的个数决定:当负因数有奇数个数,积为负;当负因数的个数为偶数个时,积为正.

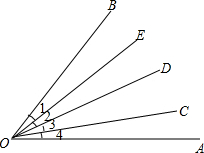 如图,∠1=∠2=∠3=∠4.
如图,∠1=∠2=∠3=∠4.