题目内容
18. 如图,已知等边△ABC,在平面上找一点P,使得△PAB、△PBC和△PAC都是等腰三角形,这样的点P的个数是( )
如图,已知等边△ABC,在平面上找一点P,使得△PAB、△PBC和△PAC都是等腰三角形,这样的点P的个数是( )| A. | 1 | B. | 4 | C. | 7 | D. | 10 |
分析 ①以A为圆心,AB为半径画弧交BC的垂直平分线于点P1,P9两点;以B为圆心,AB为半径画弧交BC的垂直平分线于点P4,这样在BC的垂直平分线上有三点;②同样在AC,AB的垂直平分线上也分别有3点;③还有一点就是AB,BC,AC三条边的垂直平分线的交点P7;相加即可得出点P的个数.
解答 解:①以A为圆心,AB为半径画弧交BC的垂直平分线于点P1,P9两点;以B为圆心,AB为半径画弧交BC的垂直平分线于点P4,这样在BC的垂直平分线上有三点,
②同样在AC,AB的垂直平分线上也分别有三点;
③还有一点就是AB,BC,AC三条边的垂直平分线的交点;
∴共3+3+3+1=10个.
故选D.
点评 本题考查了等边三角形的性质和等腰三角形的判定,线段垂直平分线性质等知识点的综合运用,解题时注意分类思想的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等;
②无理数是无限不循环小数;
③三角形的一个外角大于任何一个不相邻的内角;
④平面内点A(-1,2)与点B(-1,-2)关于x轴对称.
①两条直线被第三条直线所截,内错角相等;
②无理数是无限不循环小数;
③三角形的一个外角大于任何一个不相邻的内角;
④平面内点A(-1,2)与点B(-1,-2)关于x轴对称.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.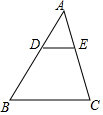 如图,在△ABC中,点D,E分别在线段AB,AC上,且DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,点D,E分别在线段AB,AC上,且DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$的值为( )
 如图,在△ABC中,点D,E分别在线段AB,AC上,且DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,点D,E分别在线段AB,AC上,且DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{2}$ |

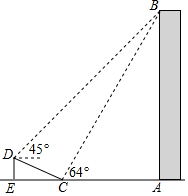 如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡度为1:$\frac{12}{5}$,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡度为1:$\frac{12}{5}$,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上. 有一个转盘,让转盘自由转动两次(指针落在分界线重新转动)
有一个转盘,让转盘自由转动两次(指针落在分界线重新转动)