题目内容
1.如图1,将一个量角器与一张等边三角形(△ABC)纸片放置成轴对称图形,CD⊥AB,垂足为D,半圆(量角器)的圆心与点D重合,此时,测得顶点C到量角器最高点的距离CE=2cm,将量角器沿DC方向平移1cm,半圆(量角器)恰与△ABC的边AC,BC相切,如图2,则AB的长为2$\sqrt{3}$cm.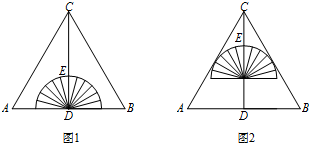
分析 如图,设图②中半圆的圆心为O,与BC的切点为M,连接OM,根据切线的性质可以得到∠OMC=90°,而根据已知条件可以得到∠DCB=30°,设AB为2xcm,根据等边三角形得到CD=$\sqrt{3}$xcm,而CE=2cm,又将量角器沿DC方向平移1cm,由此得到半圆的半径为($\sqrt{3}$x-2)cm,OC=($\sqrt{3}$x-1)cm,然后在Rt△OCM中利用三角函数可以列出关于x的方程,解方程即可求解.
解答 解:如图,设图②中半圆的圆心为O,与BC的切点为M,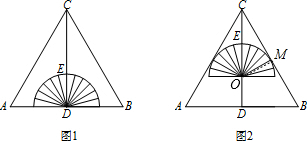 连接OM,
连接OM,
则OM⊥MC,
∴∠OMC=90°,
依题意知道∠DCB=30°,
设AB为2xcm,
∵△ABC是等边三角形,
∴CD=$\sqrt{3}$xcm,
而CE=2cm,又将量角器沿DC方向平移1cm,
∴半圆的半径为($\sqrt{3}$x-2)cm,OC=($\sqrt{3}$x-1)cm,
∴sin∠DCB=$\frac{OM}{OC}$=$\frac{1}{2}$,
∴$\frac{\sqrt{3}x-2}{\sqrt{3}x-1}$=$\frac{1}{2}$,
∴x=$\sqrt{3}$,
∴AB=2x=2$\sqrt{3}$(cm),
故答案为:2$\sqrt{3}$.
点评 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列各组代数式中,不是同类项的是( )
| A. | -x2y和5x2y | B. | 23和2 | C. | 2xy和 $\frac{3xy}{2}$ | D. | ax2和a2x |
12.(-$\frac{2}{3}$)2015•($\frac{3}{2}$)2016的计算结果是( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
16.已知两点M(3,2),N(-1,3),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为( )
| A. | (0,$-\frac{7}{4}$) | B. | ($\frac{7}{4}$,0) | C. | ($\frac{3}{2}$,0) | D. | ($\frac{7}{5}$,0) |
6.在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则树的高度为( )
| A. | 10米 | B. | 9.6米 | C. | 6.4米 | D. | 4.8米 |
 如图所示,已知BE与CD相交于F,且∠B=∠C,∠1=∠2,求证:DF=EF.
如图所示,已知BE与CD相交于F,且∠B=∠C,∠1=∠2,求证:DF=EF.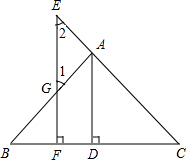 已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC.
已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC.