题目内容
15.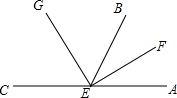 如图,EF、EG分别是∠AEB、∠BEC的平分线,求∠GEF的度数.
如图,EF、EG分别是∠AEB、∠BEC的平分线,求∠GEF的度数.
分析 由角平分线的定义可知∠GEB=$\frac{1}{2}$∠CEB,∠BEF=$\frac{1}{2}$∠AEB,然后逆用乘法的分配律可知:$\frac{1}{2}$∠CEB+$\frac{1}{2}$∠AEB=$\frac{1}{2}$(∠CEB+∠AEB)=90°.
解答 解:∵EF是∠AEB的平分线,
∴∠BEF=$\frac{1}{2}$∠AEB.
∵EG是∠BEC的平分线,
∴∠GEB=$\frac{1}{2}$∠CEB.
∴∠GEB=∠GEB+∠BEF
=$\frac{1}{2}$∠CEB+$\frac{1}{2}$∠AEB
=$\frac{1}{2}$(∠CEB+∠AEB)
=$\frac{1}{2}$×180°
=90°.
点评 本题主要考查的是平分线的定义,逆用乘法分配律以及角的和差关系求得∠GEB=$\frac{1}{2}$(∠CEB+∠AEB)是解题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
16.已知两点M(3,2),N(-1,3),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为( )
| A. | (0,$-\frac{7}{4}$) | B. | ($\frac{7}{4}$,0) | C. | ($\frac{3}{2}$,0) | D. | ($\frac{7}{5}$,0) |
5.分解因式8a2-8ab+2b2结果正确的是( )
| A. | 2(2a-b)2 | B. | 8(a-b)2 | C. | 4(a-b)2 | D. | 2(2a+b)2 |
 如图所示,已知BE与CD相交于F,且∠B=∠C,∠1=∠2,求证:DF=EF.
如图所示,已知BE与CD相交于F,且∠B=∠C,∠1=∠2,求证:DF=EF.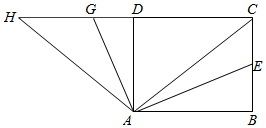
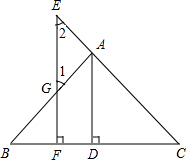 已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC.
已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC. 如图,已知 AB∥CD∥EF,AB:CD:EF=2:3:5,$\overrightarrow{BF}$=$\overrightarrow{a}$,
如图,已知 AB∥CD∥EF,AB:CD:EF=2:3:5,$\overrightarrow{BF}$=$\overrightarrow{a}$,
