题目内容
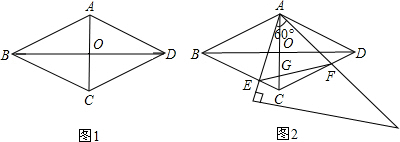
如图(1),在菱形ABCD中,AC=2,BD=2
,AC,BD相交于点O.
(1)求边AB的长;
(2)如图(2),将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G,判断△AEF是哪一种特殊三角形,并说明理由.
(3)在(2)中的旋转过程中,试说明为什么∠EAC=∠EFC.
| 3 |
(1)求边AB的长;
(2)如图(2),将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G,判断△AEF是哪一种特殊三角形,并说明理由.
(3)在(2)中的旋转过程中,试说明为什么∠EAC=∠EFC.

考点:菱形的性质,全等三角形的判定与性质,勾股定理
专题:
分析:(1)求出AO、OB,根据勾股定理求出即可;
(2)求出△ABE≌△ACF,推出AE=AF,根据等边三角形的判定推出即可;
(3)根据三角形内角和定理求出即可.
(2)求出△ABE≌△ACF,推出AE=AF,根据等边三角形的判定推出即可;
(3)根据三角形内角和定理求出即可.
解答:解:(1)∵在菱形ABCD中,AC=2,BD=2
,
∴∠AOB=90°,OA=
AC=1,BO=
BD=
,
在Rt△AOB中,由勾股定理得:AB=
=2;
(2)△AEF是等边三角形,
理由是:∵由(1)知,菱形ABCD的边长是2,AC=2,
∴△ABC和△ACD是等边三角形,
∴∠BAC=∠BAE+∠CAE=60°,
∵∠EAF=∠CAF+∠CAE=60°,
∴∠BAE=∠CAF,
在△ABE和△ACF中,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形;
(3)∵∠EAC+∠AEG+∠EGA=∠GFC+∠FCG+∠CGF=180°,∠AEG=∠FCG=60°,∠EGA=∠CGF,
∴∠EAC=∠GFC.
| 3 |
∴∠AOB=90°,OA=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
在Rt△AOB中,由勾股定理得:AB=
| AO2+BO2 |
(2)△AEF是等边三角形,
理由是:∵由(1)知,菱形ABCD的边长是2,AC=2,
∴△ABC和△ACD是等边三角形,
∴∠BAC=∠BAE+∠CAE=60°,
∵∠EAF=∠CAF+∠CAE=60°,
∴∠BAE=∠CAF,
在△ABE和△ACF中,
|
∴△ABE≌△ACF(ASA),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形;
(3)∵∠EAC+∠AEG+∠EGA=∠GFC+∠FCG+∠CGF=180°,∠AEG=∠FCG=60°,∠EGA=∠CGF,
∴∠EAC=∠GFC.
点评:本题考查了菱形的性质,全等三角形的性质和判定,等边三角形的性质和判定的应用,题目综合性比较强,有一定的难度.

练习册系列答案
相关题目
等边△ABC在数轴上的位置如图,点A、C对应的数分别为0和-1,若△ABC绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转2009次后,点B( )


| A、不对应任何数 |
| B、对应的数是2007 |
| C、对应的数是2008 |
| D、对应的数是2009 |
 如图是由若干小立方块搭成的几何体的俯视图,正方形内的数字表示在该位置上小立方块的块数,根据左视图所提供的信息,试确定x、y的值.
如图是由若干小立方块搭成的几何体的俯视图,正方形内的数字表示在该位置上小立方块的块数,根据左视图所提供的信息,试确定x、y的值. 如图,A、B两个乡镇相距21千米,原计划在两乡镇之间修一条笔直公路以改善交通状况,现在情况有变,为保护环境,县政府决定在以C处为中心方圆10千米的圆形区域内建立绿色生态旅游区,不允许公路从生态区穿过,C处距离A、B两个乡镇分别为20千米和13千米,请通过计算回答,两乡镇间的公路还能按计划实施吗?
如图,A、B两个乡镇相距21千米,原计划在两乡镇之间修一条笔直公路以改善交通状况,现在情况有变,为保护环境,县政府决定在以C处为中心方圆10千米的圆形区域内建立绿色生态旅游区,不允许公路从生态区穿过,C处距离A、B两个乡镇分别为20千米和13千米,请通过计算回答,两乡镇间的公路还能按计划实施吗? 如图:△ABC中,∠C=90°,D是AC中点,求证:AB2+3BC2=4BD2.
如图:△ABC中,∠C=90°,D是AC中点,求证:AB2+3BC2=4BD2.