题目内容
如图：△ABC中，∠C=90°，D是AC中点，求证：AB2+3BC2=4BD2．考点：勾股定理
专题：证明题
分析：根据线段中点的定义可得AC=2CD，然后在Rt△BCD中，利用勾股定理列式表示出CD，再表示出AC，再次利用勾股定理列式整理即可得证．
解答：证明：∵D是AC中点，
∴AC=2CD，
在Rt△BCD中，CD=
，
∴AC=2
，
在Rt△ABC中，AB2=AC2+BC2，
即AB2=4BD2-4BC2+BC2，
∴AB2+3BC2=4BD2．
∴AC=2CD，
在Rt△BCD中，CD=
| BD2-BC2 |
∴AC=2
| BD2-BC2 |
在Rt△ABC中，AB2=AC2+BC2，
即AB2=4BD2-4BC2+BC2，
∴AB2+3BC2=4BD2．
点评：本题考查了勾股定理，线段中点的定义，难点在于二次利用勾股定理列式整理．
练习册系列答案
口算题天天练系列答案
相关题目
某工人原计划每天生产a个零件，现实际每天多生产b个零件，则生产m个零件提前的天数为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
星期天8：00～8：30，燃气公司给平安加气站的储气罐注入天然气．之后，一位工作人员以每车20米3的加气量，依次给在加气站排队等候的若干辆车加气．储气罐中的储气量y（米3）与时间x（小时）的函数关系如图所示．
在如图方格纸中平移四边形ABCD，使点A移到点A′，使点B移到点B′，使点C移到点C′，使点D移到点D′，画出平移后的四边形A′B′C′D′．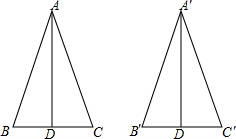
如图，AD、A′D′分别是△ABC和△A′B′C′的边BC、B′C′上的高，且AD=A′D′，AB=A′B′，∠BAC=∠B′A′C′．