题目内容
 如图,A、B两个乡镇相距21千米,原计划在两乡镇之间修一条笔直公路以改善交通状况,现在情况有变,为保护环境,县政府决定在以C处为中心方圆10千米的圆形区域内建立绿色生态旅游区,不允许公路从生态区穿过,C处距离A、B两个乡镇分别为20千米和13千米,请通过计算回答,两乡镇间的公路还能按计划实施吗?
如图,A、B两个乡镇相距21千米,原计划在两乡镇之间修一条笔直公路以改善交通状况,现在情况有变,为保护环境,县政府决定在以C处为中心方圆10千米的圆形区域内建立绿色生态旅游区,不允许公路从生态区穿过,C处距离A、B两个乡镇分别为20千米和13千米,请通过计算回答,两乡镇间的公路还能按计划实施吗?考点:勾股定理的应用
专题:
分析:过点C作CD⊥AB于D,设AD=x,表示出DB,再利用勾股定理列出表示出CD2,然后解方程求出x,再利用勾股定理列式求出CD,然后根据CD的长度判断即可.
解答: 解:如图,过点C作CD⊥AB于D,
解:如图,过点C作CD⊥AB于D,
设AD=x,则DB=21-x,
在Rt△ACD中,CD2=AC2-AD2=202-x2,
在Rt△BCD中,CD2=BC2-BD2=132-(21-x)2,
∴202-x2=132-(21-x)2,
整理得,42x=672,
解得x=16,
所以,CD=
=
=12,
∵12>10,
∴两乡镇间的公路能按计划实施.
 解:如图,过点C作CD⊥AB于D,
解:如图,过点C作CD⊥AB于D,设AD=x,则DB=21-x,
在Rt△ACD中,CD2=AC2-AD2=202-x2,
在Rt△BCD中,CD2=BC2-BD2=132-(21-x)2,
∴202-x2=132-(21-x)2,
整理得,42x=672,
解得x=16,
所以,CD=
| AC2-AD2 |
| 202-162 |
∵12>10,
∴两乡镇间的公路能按计划实施.
点评:本题考查了勾股定理的应用,作出辅助线构造成两个直角三角形是解题的关键,难点在于根据CD的长列出方程.

练习册系列答案
相关题目
下列各题计算正确的是( )
| A、(a-3b)(-6a)=-6a2-18ab | ||
B、(-
| ||
C、(-
| ||
| D、-3x(2x2-x+1)=-6x3+3x2-3x |
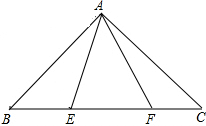 已知如图,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2.
已知如图,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点且∠EAF=45°,求证:EF2=BE2+FC2.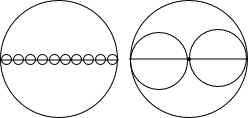 如图,两个大小相同的大圆,其中一个大圆内有10个小圆,另一个大圆内有2个小圆,你认为大圆内的10个小圆的周长之和与另一个大圆内的2个小圆的周长之和哪一个大?请你猜一猜,并用学过的知识和数学方法验证你的猜想.
如图,两个大小相同的大圆,其中一个大圆内有10个小圆,另一个大圆内有2个小圆,你认为大圆内的10个小圆的周长之和与另一个大圆内的2个小圆的周长之和哪一个大?请你猜一猜,并用学过的知识和数学方法验证你的猜想.
 如图,AB,AC为⊙O的两条弦,且AB=AC,D为
如图,AB,AC为⊙O的两条弦,且AB=AC,D为
 星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示.
星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20米3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(米3)与时间x(小时)的函数关系如图所示. 某水渠的横截面如图,BC∥AD,斜坡AB长2.2m,坡角∠BAD=68°,气象部门预测今年雨水可能增大,经工程技术人员论证,当坡角不超过50°时,可确保安全.决定对其进行改造,坡脚A不动,坡顶B沿BC削到点F处.问BF至少是多少米?(精确到0.01m)
某水渠的横截面如图,BC∥AD,斜坡AB长2.2m,坡角∠BAD=68°,气象部门预测今年雨水可能增大,经工程技术人员论证,当坡角不超过50°时,可确保安全.决定对其进行改造,坡脚A不动,坡顶B沿BC削到点F处.问BF至少是多少米?(精确到0.01m)