题目内容
7.当n取何值时,$y=({n}^{2}+2n){x}^{{n}^{2}+n-1}$是反比例函数?它的图象在哪些象限内?在每个象限内,y随x的变化情况是怎样的?分析 根据反比例函数的定义得到n2+n-1=-1,由此求得n的值;然后求系数(n2+2n)的值,根据它的符号来判定该双曲线的性质.
解答 解:∵$y=({n}^{2}+2n){x}^{{n}^{2}+n-1}$是反比例函数,
∴n2+n-1=-1,
解得 n=0(舍去),或n=-1.
即当n=-1时,$y=({n}^{2}+2n){x}^{{n}^{2}+n-1}$是反比例函数.
当n=-1时,n2+2n=1-2=-1<0,
所以该函数图象经过第二、四象限,且在每一象限内,y随x的增大而增大.
点评 本题考查了反比例函数的定义和反比例函数的性质.判断一个函数是否是反比例函数,首先看看两个变量是否具有反比例关系,然后根据反比例函数的意义去判断,其形式为y=$\frac{k}{x}$(k为常数,k≠0)或y=kx-1(k为常数,k≠0).

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
17. 如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
 如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )| A. | 10 | B. | 12 | C. | 18 | D. | 24 |

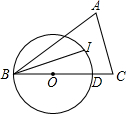 如图,△ABC中,AC=BC,I为△ABC的内心,O为BC上一点,过B、I两点的⊙O交BC于D点,tan∠CBI=$\frac{1}{3}$,AB=6
如图,△ABC中,AC=BC,I为△ABC的内心,O为BC上一点,过B、I两点的⊙O交BC于D点,tan∠CBI=$\frac{1}{3}$,AB=6