题目内容
5．若|2a-5|与$\sqrt{b+2}$互为相反数，则a=$\frac{5}{2}$，b=-2．分析 根据互为相反数的两个数的和等于0列出方程，然后根据非负数的性质列方程求解即可．
解答 解：∵|2a-5|与$\sqrt{b+2}$互为相反数，
∴|2a-5|+$\sqrt{b+2}$=0，
∴2a-5=0，b+2=0，
解得a=$\frac{5}{2}$，b=-2．
故答案为：$\frac{5}{2}$；-2．
点评 本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
相关题目
16．（1）$\sqrt{18}$×$\sqrt{\frac{1}{2}}$÷$\sqrt{3}$
（2）$\sqrt{8}$+2$\sqrt{3}$-（$\sqrt{27}$-$\sqrt{2}$）
（2）$\sqrt{8}$+2$\sqrt{3}$-（$\sqrt{27}$-$\sqrt{2}$）
20．关于点到直线的距离的四种说法正确的是（ ）
| A． | 连接直线外的点和直线上的点的线段叫做点到直线的距离 | |
| B． | 连接直线外的点和直线上的点的线段的长度叫做点到直线的距离 | |
| C． | 直线外一点到这条直线的垂线段叫做这点到直线的距离 | |
| D． | 直线外一点到这条直线的垂线段的长度叫做这点到直线的距离 |
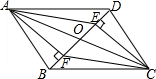如图，在四边形ABCD中，AB=CD，BE=DF；AE⊥BD，CF⊥BD，对角线AC、BD相交于点O，求证：AO=CO．
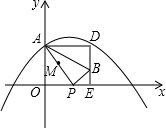如图，在平面直角坐标系xOy中，抛物线y=ax2+$\frac{5}{6}$x+c过点A（0，4）和C（8，0），P（t，0）是x轴正半轴上的一个动点，M是线段AP的中点，将线段MP绕点P顺时针旋转90°得线段PB．过点B作x轴的垂线、过点A作y轴的垂线，两直线相交于点D．