题目内容
12.已知点C,D在以AB为直径的圆O上,且CD平分∠ACB,若AB=4,∠CBA=15°,求CD的长.分析 过点O作OE⊥CD,连接OC,根据AB为直径得出∠ACB=90°,再根据角平分线得出∠BCD=45°,由∠CBA=15°,得∠OCB=15°,即可得出∠OCE=30°,由直角三角形的性质得出OE,从而得出CE,由垂径定理得出CD即可.
解答  解:过点O作OE⊥CD,连接OC,
解:过点O作OE⊥CD,连接OC,
∴CE=DE,
∵AB为直径,
∴∠ACB=90°,
∵CD平分∠ACB,
∴∠BCD=45°,
∵∠CBA=15°,
∴∠OCB=15°,
∴∠OCE=30°,
∴OE=$\frac{1}{2}$OC,
∵AB=4,
∴OC=2,
∴OE=1,
∴CE=$\sqrt{O{C}^{2}-O{E}^{2}}$=$\sqrt{4-1}$=$\sqrt{3}$,
∴CD=2$\sqrt{3}$.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了勾股定理和三角形相似的判定与性质.

练习册系列答案
相关题目
2.在-3.14,$\sqrt{2}$,0,π,0.1010010001…,$\sqrt{16}$中,无理数共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
9.一组互不相同的数据3、4、6、7、x的中位数是x,若这组数据都是整数,这组数据中的x是( )
| A. | 4 | B. | 6 | C. | 5 | D. | 8 |
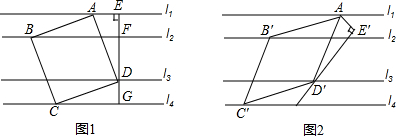





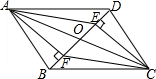 如图,在四边形ABCD中,AB=CD,BE=DF;AE⊥BD,CF⊥BD,对角线AC、BD相交于点O,求证:AO=CO.
如图,在四边形ABCD中,AB=CD,BE=DF;AE⊥BD,CF⊥BD,对角线AC、BD相交于点O,求证:AO=CO.