题目内容
3. 如图,Rt△ABC的角平分线AD与BE相交于F,M是DE的中点,设FM=2.5,S△DEF=15,求CD,AB的长.
如图,Rt△ABC的角平分线AD与BE相交于F,M是DE的中点,设FM=2.5,S△DEF=15,求CD,AB的长.
分析 在AB上取两点H、O,使AE=AH,BO=BD,连接FH、FO,延长FM至L,使LM=FM,连接EL,过E作EG⊥MN,交NM的延长线于点G,作FK⊥AC于K,FJ⊥BC于J.首先证明△EGF≌△FNH,推出HO=5,FN=EG=6,再在△FHO中,解三角形求出FH、OF,利用勾股定理求出DJ、EK,利用MJ∥AC,得到$\frac{DJ}{CJ}$=$\frac{DF}{AF}$,求出AF,由FK∥BC,得$\frac{EK}{CK}$=$\frac{EF}{BF}$,求出BF,再由勾股定理求出AN、BN即可解决问题.
解答 证明:在AB上取两点H、O,使AE=AH,BO=BD,连接FH、FO,延长FM至L,使LM=FM,连接EL,过E作EG⊥MN,交NM的延长线于点G,作FK⊥AC于K,FJ⊥BC于J.得△AEF≌△AHF,则∠AFH=∠AFE=45°,
同理得:∠BFD=∠BFO=45°,
∴∠HFO=180°-45°-45°-45°=45°,
得△EML≌△DMF,则EL=DF,∠LEM=∠FDM,
∵∠BFD=∠FED+∠FDM=45°,
∴∠FED+∠LEM=45°,
即∠LEF=45°,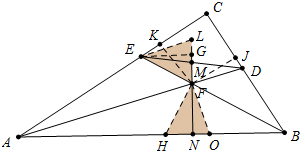
∴∠LEF=∠HFO=45°,
∵EF=FH,OF=FD=EL,
∴△LEF≌△OFH,
∴∠EFM=∠FHN,
过E作EG⊥MN,交NM的延长线于点G,
∵∠GEF+∠EFG=90°,∠EFG+∠HFN=90°,
∴∠GEF=∠HFN,
∴△EGF≌△FNH,
∴EG=FN,
∵M是DE的中点,
∴S△DEF=2S△EFM=2×$\frac{1}{2}$×FM•EG=FM•EG=15,
∵FM=$\frac{5}{2}$,
∴EG=6,
∴FN=EG=6.
把△FHO放大,下图中,作OT⊥FH于T,OT交FN于R.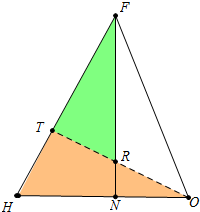
∵∠TFO=∠TOF=45°,
∴TF=TO,
∵∠TFR+∠H=90°,∠H+∠HOT=90°,
∴∠TFR=∠TOH,∵∠FTR=∠OTH=90°,
∴△FTR≌△OTH,
∴TH=TR,FR=HC=5,
∴RN=1,设TH=TR=a,OR=y,
由△ORN∽△FRT,得$\frac{RN}{TR}$=$\frac{RO}{FR}$,
∴$\frac{1}{a}$=$\frac{y}{5}$,
∴ay=5 ①
在Rt△HTO中,∵HT2+OT2=OH2,
∴a2+(a+y)2=52 ②,
由①②可得a=$\sqrt{5}$或$\frac{\sqrt{10}}{2}$,
当a=$\sqrt{5}$时,则FH=3$\sqrt{5}$,OF=2$\sqrt{10}$,
∵FN=MJ=MK=6,
∴EK=$\sqrt{E{F}^{2}-F{K}^{2}}$=$\sqrt{(3\sqrt{5})^{2}-{6}^{2}}$=3,DJ=$\sqrt{D{F}^{2}-M{J}^{2}}$=$\sqrt{(2\sqrt{10})^{2}-{6}^{2}}$=2,
易知四边形CKFJ是正方形,
∴CK=CJ=6,CD=CJ+DJ=8,
∵MJ∥AC,
∴$\frac{DJ}{CJ}$=$\frac{DF}{AF}$,
∴$\frac{2}{6}$=$\frac{2\sqrt{10}}{AF}$,
∴AF=6$\sqrt{10}$,
∴AN=$\sqrt{A{F}^{2}-F{N}^{2}}$=18,
∵FK∥BC,
∴$\frac{EK}{CK}$=$\frac{EF}{BF}$,
∴$\frac{3}{6}$=$\frac{3\sqrt{5}}{BF}$,
∴BF=6$\sqrt{5}$,
∴BN=$\sqrt{B{F}^{2}-F{N}^{2}}$=12,
∴AB=18+12=30,
当a=$\frac{\sqrt{10}}{2}$时,则FH=2$\sqrt{10}$,OF=3$\sqrt{5}$,
∵FN=MJ=MK=6,
∴EK=$\sqrt{E{F}^{2}-F{K}^{2}}$=2,DJ=$\sqrt{D{F}^{2}-M{J}^{2}}$=3,
易知四边形CKFJ是正方形,
∴CK=CJ=6,CD=CJ+DJ=9,
∵MJ∥AC,
∴$\frac{DJ}{CJ}$=$\frac{DF}{AF}$,
∴$\frac{3}{6}$=$\frac{3\sqrt{5}}{AF}$
∴AF=6$\sqrt{5}$,
∴AN=$\sqrt{A{F}^{2}-F{N}^{2}}$=12,
∵FK∥BC,
∴$\frac{EK}{CK}$=$\frac{EF}{BF}$,
,∴$\frac{2}{6}$=$\frac{2\sqrt{10}}{BF}$,
∴BF=6$\sqrt{10}$,
∴BN=$\sqrt{B{F}^{2}-F{N}^{2}}$=18,
∴AB=18+12=30,
综上所述,AB=30,CD=8或9.
点评 本题考查角平分线性质定理、全等三角形的判定和性质、平行线垂线段成比例定理、勾股定理等知识,解题的关键是学会添加辅助线,构造全等三角形,特殊三角形解决问题,题目比较难,辅助线比较多,属于竞赛题目.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 42的算术平方根为4 | B. | 2的算术平方根为$\sqrt{2}$ | ||
| C. | $\sqrt{{3}^{2}}$的算术平方根是$\sqrt{3}$ | D. | $\sqrt{81}$的算术平方根是9 |
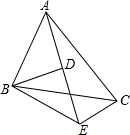 如图,$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$,且∠CBE=25°,求∠ABD的度数.
如图,$\frac{AB}{BD}$=$\frac{BC}{BE}$=$\frac{CA}{ED}$,且∠CBE=25°,求∠ABD的度数. 如图,长方体的长、宽、高分别是9cm,7cm,8cm,一只蚂蚁沿着长方体的表面从点A爬到点B,则蚂蚁爬行的最短路径长$\sqrt{296}$.
如图,长方体的长、宽、高分别是9cm,7cm,8cm,一只蚂蚁沿着长方体的表面从点A爬到点B,则蚂蚁爬行的最短路径长$\sqrt{296}$.