题目内容
16.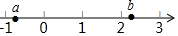 已知a,b在数轴上的位置如图所示,化简代数式$\sqrt{(a-1)^{2}}$-$\sqrt{(a+b)^{2}}$+|1-b|的结果等于( )
已知a,b在数轴上的位置如图所示,化简代数式$\sqrt{(a-1)^{2}}$-$\sqrt{(a+b)^{2}}$+|1-b|的结果等于( )| A. | -2a | B. | -2b | C. | -2a-b | D. | 2 |
分析 先根据数轴得出a<0<b,且|a|<1,|b|>2,进而利用二次根式的性质和绝对值的性质化简得出即可.
解答 解:由题意,可得a<0<b,且|a|<1,|b|>2,
所以$\sqrt{(a-1)^{2}}$-$\sqrt{(a+b)^{2}}$+|1-b|
=1-a-(a+b)+(b-1)
=1-a-a-b+b-1
=-2a.
故选A.
点评 此题主要考查了实数与数轴,二次根式的性质与化简,绝对值的性质,正确化简是解题关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
7.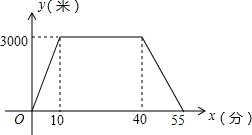 娟娟同学上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.娟娟同学离家的路程y(m)和所经过的时间x(min)之间的函数图象如图所示,则下列说法不正确的是( )
娟娟同学上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.娟娟同学离家的路程y(m)和所经过的时间x(min)之间的函数图象如图所示,则下列说法不正确的是( )
 娟娟同学上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.娟娟同学离家的路程y(m)和所经过的时间x(min)之间的函数图象如图所示,则下列说法不正确的是( )
娟娟同学上午从家里出发,骑车去一家超市购物,然后从这家超市返回家中.娟娟同学离家的路程y(m)和所经过的时间x(min)之间的函数图象如图所示,则下列说法不正确的是( )| A. | 娟娟同学与超市相距3000m | |
| B. | 娟娟同学去超市途中的速度是300m/min | |
| C. | 娟娟同学在超市逗留了30min | |
| D. | 娟娟同学从超市返回家比从家里去超市的速度快 |
11. 张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )
张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )
 张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )
张老师在黑板上画出了如图所示的图形,已知∠BAC=90°,AD⊥BC,垂足为D,则下列说法错误的是( )| A. | ∠BAC与∠B是同旁内角 | B. | AB与AC互相垂直 | ||
| C. | 点A与直线BC的垂线段为线段AD | D. | 点A到BC的距离是线段AD |
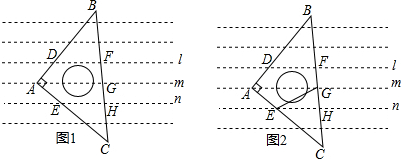
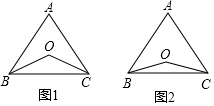
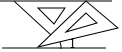 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含45°角的直角三角板的斜边与纸条一边重合,含30°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )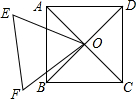 如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转,在旋转过程中,当CF=DE时,∠DOF的大小是165°或15°.
如图,正方形ABCD的对角线相交于点O,正三角形OEF绕点O旋转,在旋转过程中,当CF=DE时,∠DOF的大小是165°或15°.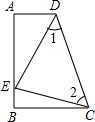 如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.