题目内容
6.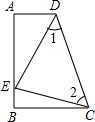 如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.(1)求证:Rt△ADE与Rt△BEC全等;
(2)求证:△CDE是直角三角形.
分析 (1)估计等边对等角,推出DE=EC,再根据HL即可证明Rt△ADE≌Rt△BEC;
(2)由Rt△ADE≌Rt△BEC,推出∠AED=∠BCE,由∠ECB+∠BEC=90°,推出∠AED+∠BEC=90°.即∠DEC=90°;
解答 解:(1)全等.理由是:
∵∠1=∠2,
∴DE=CE,
∵∠A=∠B=90°,AE=BC,
在Rt△ADE和Rt△BEC中,
$\left\{\begin{array}{l}{AE=BC}\\{DE=EC}\end{array}\right.$,
∴Rt△ADE≌Rt△BEC(HL).
(2)是直角三角形.理由是:
∵Rt△ADE≌Rt△BEC,
∴∠AED=∠BCE,
∵∠ECB+∠BEC=90°,
∴∠AED+∠BEC=90°.
∴∠DEC=90°,
∴△CDE是直角三角形.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是正确寻找全等三角形的条件,灵活运用全等三角形的性质解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.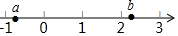 已知a,b在数轴上的位置如图所示,化简代数式$\sqrt{(a-1)^{2}}$-$\sqrt{(a+b)^{2}}$+|1-b|的结果等于( )
已知a,b在数轴上的位置如图所示,化简代数式$\sqrt{(a-1)^{2}}$-$\sqrt{(a+b)^{2}}$+|1-b|的结果等于( )
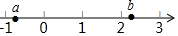 已知a,b在数轴上的位置如图所示,化简代数式$\sqrt{(a-1)^{2}}$-$\sqrt{(a+b)^{2}}$+|1-b|的结果等于( )
已知a,b在数轴上的位置如图所示,化简代数式$\sqrt{(a-1)^{2}}$-$\sqrt{(a+b)^{2}}$+|1-b|的结果等于( )| A. | -2a | B. | -2b | C. | -2a-b | D. | 2 |
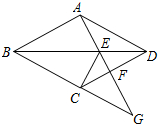 如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE.
如图,四边形ABCD是菱形,点G是BC延长线上一点,连结AG,分别交BD、CD于点E、F,连结CE. 如图,已知菱形ABCD的周长为16,∠B=120°,求这个菱形的面积.
如图,已知菱形ABCD的周长为16,∠B=120°,求这个菱形的面积.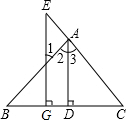 如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,试说明AD平分∠BAC.完成下面推理过程:
如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,试说明AD平分∠BAC.完成下面推理过程:
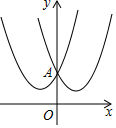 如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图所示二次函数y1=x2+2x+2与y2=x2-2x+2是“关于y轴对称二次函数”.
如果两个二次函数的图象关于y轴对称,我们就称这两个二次函数互为“关于y轴对称二次函数”,如图所示二次函数y1=x2+2x+2与y2=x2-2x+2是“关于y轴对称二次函数”.